2015杭州中考:“不同寻常”压轴题引发思考
2015年中考已经在全国各地接近尾声,各地中考压轴题让人“眼花缭乱”,考查考生的综合能力同时,一些问题不得不引起教学一线教师的思考。
我们先看2015年浙江杭州第23题:
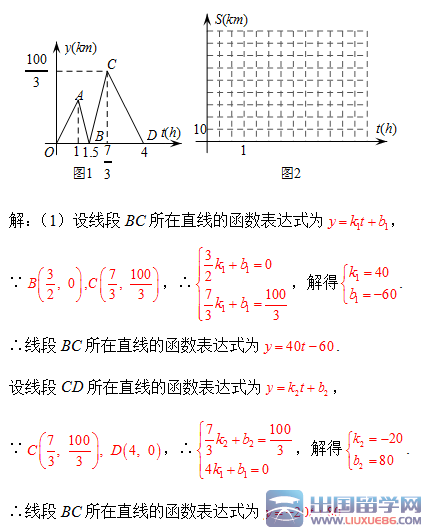
方成同学看到一则材料,甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,方成思考后发现了图1的部分正确信息,乙先出发1h,甲出发0.5小时与乙相遇,??,请你帮助方成同学解决以下问题:
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20
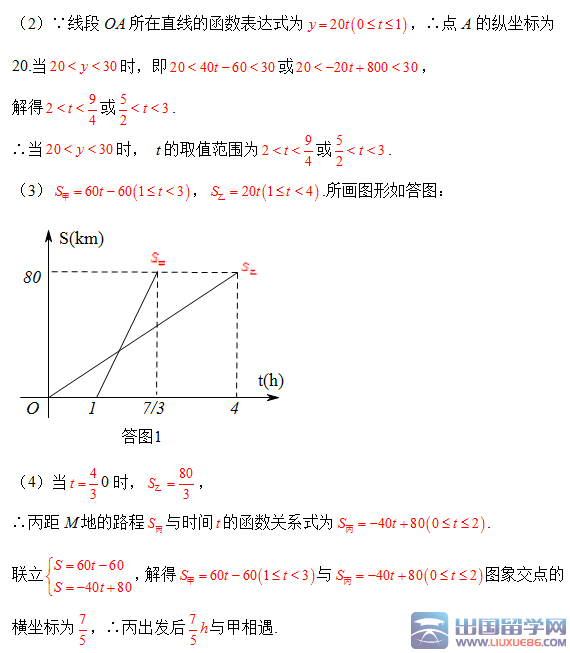
(3)分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
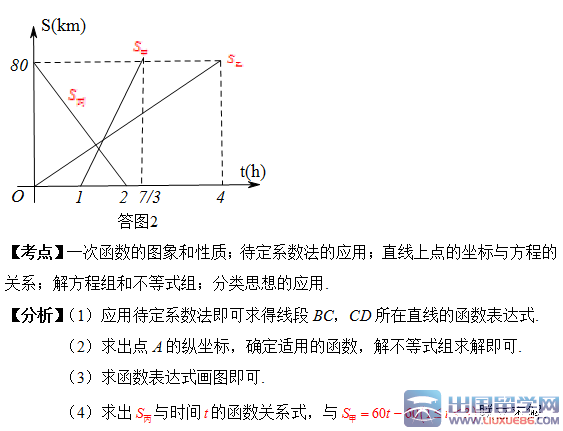
(4)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过
h与乙相遇,问丙出发后多少时间与甲相遇.
为什么说此题会“不同寻常”?我们很多人已经习惯压轴题是函数、几何、动态等综合题。突然出现此类应用题型,确实出乎很多人意料,以让杭城很多考生感叹说今年中考的数学“简单了”。
这也给我们很多教学一线教师一个提示,教无定法,让学生以不变应万变,只有掌握深厚的数学知识,才能在中考中取得好成绩。
应用题题型一般和方程都有关,我们知道方程是贯穿初中代数的一条知识主线,方程型综合题一直是中考命题的热点,也是中考试题中常见的中档题。这类试题主要是结合代数式的恒等变形,求代数式的值,或通过解方程(组)、解不等式(组),利用函数知识求参数的值或取值范围,证明与方程有关的代数式解。
方程是研究数量关系的重要工具。在处理生活中实际问题时,根据已知与未知量之间的联系及相等关系建立方程或方程组,从而使问题获得解决的思想方法称为方程思想。
运用方程思想解题的一般步骤为:
(1)把问题归结为确定一个或几个未知数;
(2)挖掘问题中已知与未知数量之间的等量关系,建立方程或方程组;
(3)求解或讨论所得方程或方程组;
(4)检验并作出符合问题实际的回答。
方程是研究数量关系的重要工具。在处理生活中实际问题时,根据已知与未知量之间的联系及相等...