圆与圆的位置关系是怎样的,又有几种关系呢?不清楚的考生赶紧看过来,下面由出国留学网小编为你精心准备了“圆与圆的位置关系是怎样的?”,持续关注本站将可以持续获取更多的考试资讯!
圆与圆的位置关系是怎样的?
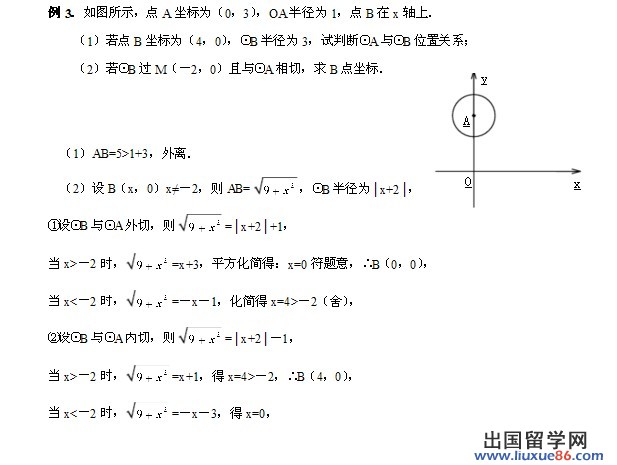
圆与圆的位置关系:外离、相切(内切和外切)、相交、内含。在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。
一、圆与圆的位置关系的判断方法
1、设两个圆的半径为R和r,圆心距为d。
则有以下五种关系:
1、d>R+r 两圆外离; 两圆的圆心距离之和大于两圆的半径之和。
2、d=R+r 两圆外切; 两圆的圆心距离之和等于两圆的半径之和。
3、d=R-r 两圆内切; 两圆的圆心距离之和等于两圆的半径之差。
4、d
5、d
2、圆和圆的位置关系,还可用有无公共点来判断:
1、无公共点,一圆在另一圆之外叫外离,在之内叫内含。
2、有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切。
3、有两个公共点的叫相交。两圆圆心之间的距离叫做圆心距。
二、扩展资料
1、点和圆位置关系
①P在圆O外,则 PO>r。
②P在圆O上,则 PO=r。
③P在圆O内,则 PO
反之亦然。
平面内,点P(x0,y0)与圆(x-a)²+(y-b)²=r²的位置关系判断一般方法是:
①如果(x0-a)²+(y0-b)²
②如果(x0-a)²+(y0-b)²=r²,则P在圆上。
③如果(x0-a)²+(y0-b)²>r²,则P在圆外。
2、直线和圆位置关系
①直线和圆无公共点,称相离。 AB与圆O相离,d>r。
②直线和圆有两个公共点,称相交,这条直线叫做圆的割线。AB与⊙O相交,d
③直线和圆有且只有一公共点,称相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。圆心与切点的连线垂直于切线。AB与⊙O相切,d=r。(d为圆心到直线的距离)
推荐阅读: