财务数值技术
数值分析
数值分析
快速分析图形资料的数值
【阅读提示】公务员考试《行政职业能力测验》科目资料分析模块图形资料题可以通过“定性分析”图形的高低、长短来巧测其数据的大小与增减幅度。本文中国家公务员网归纳了三类“定性分析”运用技巧。
在公务员考试《行政职业能力测验》科目资料分析模块图形型材料中,很多结论可以通过图形自身的性质得到:
一、柱状图、趋势图中数据的大小可以通过“柱”的长短或“点”的高低来判定。
二、柱状图、趋势图中数据的增减可以通过“柱”的长度增减或“点”的高低变化来判定。
三、饼图中数据或者比例的大小可以通过所占扇形的大小来判定。某些比例的大小可以通过目测大致比例得到。
求函数值域的方法
函数值域是什么,怎么求?不清楚的小伙伴看过来,下面由出国留学网小编为你精心准备了“求函数值域的方法”仅供参考,持续关注本站将可以持续获取更多的资讯!
求函数值域的方法
值域
域为数学名词,函数经典定义中,因变量改变而改变的取值范围叫做这个函数的值域,在函数现代定义中是指定义域中所有元素在某个对应法则下对应的所有的象所组成的集合。
函数值域的求法
1、配方法:转化为二次函数,利用二次函数的特征来求值;常转化为型如: 的形式;
2、逆求法(反求法):通过反解,用 来表示 ,再由 的取值范围,通过解不等式,得出 的取值范围;常用来解,型如: ;
3、换元法:通过变量代换转化为能求值域的函数,化归思想;
4、三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求值域;
5、基本不等式法:转化成型如: ,利用平均值不等式公式来求值域;
6、单调性法:函数为单调函数,可根据函数的单调性求值域。
7、数形结合:根据函数的几何图形,利用数型结合的方法来求值域。
8、定义法:已知某个三角函数的定义值域,通过转化成三角函数来求解该函数的值域
9、画图法:这种方法简单快捷,只要将函数图形画出来,一眼就能看到函数的值域。
拓展阅读:函数最小正周期怎么求
所谓的函数的最小正周期,一般在高中时期的话遇到的都是那种特殊形式的函数,比如;f(a-x)=f(x+a),这个函数的最小周期就是T=(a-x+x+a)/2=a。还有是三角函数y=A sin(wx+b)+t,最小正周期就是T=2帕/w。
最小正周期求法
1、公式法
这类题目是通过三角函数的恒等变形,转化为一个角的一种函数的形式,用公式去求,其中正余弦函数求最小正周期的公式为T=2π/|ω| ,正余切函数T=π/|ω|。
函数f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)(A≠0,ω>0)的最小正周期都是;函数f(x)=Atan(ωx+φ)和f(x)=Acot(ωx+φ)(A≠0,ω>0)的最小正周期都是,运用这一结论,可以直接求得形如y=Af(ωx+φ)(A≠0,ω>0)一类三角函数的最小正周期(这里“f”表示正弦、余弦、正切或余切函数)。
例3、求函数y=cotx-tanx的最小正周期.
解:y=1/tanx-tanx=(1-tan^2· x)/tanx=2*(1-tan^2·x)/(2tanx)=2cot2x
∴T=π/2
函数为两个三角函数相加,若角频率之比为有理数,则函数有最小正周期。
2、最小公倍数法
设f(x)与g(x)是定义在公共集合上的两个三角周期函数,T1、T2分别是它们的周期,且T1≠T2,则f(x)±g(x)的最小正周期T1、T2的最小公倍数,分数的最小公倍数=T1,T2分子的最小公倍...
高考地理复习资料:昼夜数值体现昼夜长短
今天我们要复习的是昼夜数值体现昼夜长短,这类知识点要多记忆哦!一些大题会考到!
高考地理复习资料:昼夜数值体现昼夜长短
昼夜数值体现昼夜长短:
在考察的题目中昼夜长短也会以数值的方式体现。昼夜等长,各12小时;
如果昼长大于12小时,说明昼长夜短;
如果昼长小于于12小时,说明昼短夜长。
赤道始终昼夜平分,昼夜差为0,纬度越高,昼夜长短差越大。
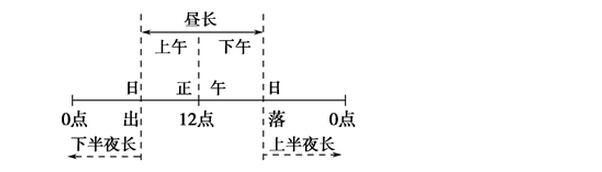
日出日落时间与昼夜长短:昼长=日落-日出。
小编精心为您推荐:
南京信息工程大学2019考研大纲:T04数值分析
考研大纲频道为大家提供南京信息工程大学2019考研大纲:T04数值分析,一起来学习一下吧!更多考研资讯请关注我们网站的更新!
南京信息工程大学2019考研大纲:T04数值分析
科目代码:T04
科目名称:数值分析
第一部分 大纲内容
一、绪论
1. 误差的来源与分类、误差
2. 有效数字,误差的定性分析与避免误差的危害、算法的数值稳定性
二、插值法
1. 拉格朗日插值公式、牛顿插值公式,插值余项、误差估计
2. 带导数的插值,插值余项、误差估计
3. 等距节点插值,插值余项、误差估计
4. 分段低次插值、插值余项、误差估计
三、曲线拟合与平方逼近
1. 函数逼近,正交多项式,有理逼近的概念
2. 最佳平方逼近
3. 曲线拟合的最小二乘法
四、数值积分与数值微分
1. 数值积分公式的一般形式及导出方法
2. 插值型求积公式、几种低阶求积公式及余项
3. 代数精度
4. 数值微分方法的基本思想,高斯-勒让德等求积公式,多重积分,数值微分公式
五、常微分方程数值解法
1. Euler法、Euler 法的改进、龙格-库塔方法
2. 单步法和多步法的相容性、收敛性和稳定性
3. 离散变量法和离散误差
4. 线性多步法的相容性、收敛性和稳定性
六、非线性方程求根
1. 迭代法的基本思想、迭代过程的收敛性、迭代过程的收敛速度、迭代过程的加速原理;
2. 牛顿法及其收敛性
3. 弦截法及其应用;
七、线性方程组的直接解法
1. 高斯消去法、高斯列主元消去法,直接法的优缺点
2. LU三角分解法、平方根法、追赶法;
3. 向量和矩阵的范数、矩阵的谱半径、条件数和线性方程组解的误差的关系
八、线性方程组迭代解法
1. 雅可比迭代法、高斯—塞德尔迭代法、SOR迭代法
2. 矩阵谱范数的计算方法,迭代法的收敛性判定方法
3. 线性方程组迭代解法的应用
九、矩阵特征值问题
1. 幂法和反幂法的原理和解决的对象及其加速方法
2. 矩阵的QR法分解的原理和变形和同时过程
3. 特征值的估计,正交变换的Givens和Householder变换
第二部分 说明
1、基本要求:掌握基本计算方法的原理和使用, 各种计算方法的理论分...
2013中考数学备考:函数值(一轮复习)
推荐更多