二、考题解析
初中数学《多边形的内角和》主要教学过程及板书设计
教学过程
(一)设疑导入,引出新课
我们知道,三角形内角和等于180°,正方形、长方形的内角和都等于360°,那么,任意一个四边形的内角和是否也等于360°呢?你能利用三角形内角和定理证明任意四边形内角和等于360°吗?
(二)合作探究,解决问题
活动一:学生分小组探究四边形内角和,小组展示探究结果与方法。
最后教师引导学生一同归纳总结。
从一个顶点出发引对角线的方法,构建成两个三角形,利用三角形内角和求解四边形内角和。
活动二:类比上面的过程,你能推导出五边形和六边形的内角和各是多少吗?
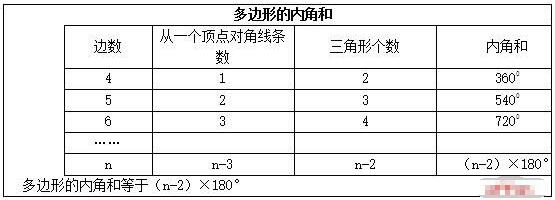
通过以上过程,从n边形的一个顶点出发,可以做(n-3)条对角线,他们将n边形分成(n-2)个三角形,n边形内角和等于180°×(n-2)。归纳出n边形内角和公式。
利用多边形内角和公式在求解过程中,已知多边形内角和可求多边形的边有几条,已知多边形边的条数可求多边形内角和。
(三)例题巩固,理解原理
PPT出示例题:如果一个四边形的一组对角互补,那么另一组对角有什么关系?
师生活动:学生先独立完成例题,老师对例题进行讲解。
(四)综合应用,深化原理
1.一个多边形每一个内角都是144°,求这个多边形的边数?
2.一个多边形的内角和是990°,求这个多边形的边数。
(五)小结作业
教师引导学生回顾本节课所学的主要内容,通过相互交流分享观点:
(1)多边形内角和公式推导方法是什么?(2)多边形内角和公式是什么
作业:课后练习题并思考多边形的外角和是多少?
板书设计
答辩题目解析
1.在教学讲“多边形分割成几个三角形”时,如何做到不重不漏?
【参考答案】
在教学过程中,我首先让学生从四边形、五边形、六边形入手,试着连一连,画一画,发现其中的规律。然后引导学生思考因从一个顶点出发,与左右相邻的的两个顶点连线,不能构成三角形,所以要提醒学生注意按照逆时针或者顺时针方向依次连接各顶点,以免会重复或遗漏。
2.n边形多角线公式是什么?
【参考答案】

教师资格证考试栏目推荐:
| 教师资格证题库 | 教师考试备考辅导 | 教育学资料 | 教育心理学资料 | 综合素质资料 | 教育知识与能力 |