今天小编为大家提供行测数量关系:数学运算统筹问题要学会选择最优,希望大家能够运用最优思想来解决这类问题!祝你考试顺利!
行测数量关系:数学运算统筹问题要学会选择最优
数学运算统筹问题在行测考试中虽不多见但在考试中一旦出现,往往能成为拉分题,所以掌握这种题型一旦考试遇到就能成为你考试的优势。做好统筹问题的关键就在于要有最优思想,在各种情况下选择最优方案进行求解。小编介绍在两种常见统筹问题中如何选择最优。
一、时间安排问题
在时间安排问题中所谓选择最优就是要选择时间最短的情况。如何做到时间最短呢?就需要重复利用的时间尽可能多。
例1.妈妈给客人沏茶。洗开水壶需要1分钟,烧水需要15分钟,洗茶壶需要1分钟,洗茶杯需要1分钟,拿茶叶需要2分钟,依照最合理的安排,要几分钟就能沏好茶:
A.16分钟 B.17分钟 C.18分钟 D.19分钟
解析:在烧水的同时可以同时洗好茶壶、茶杯和拿好茶叶,但烧水和洗开水壶不能同时进行,洗开水壶必须在前,烧水在后。故最少使用1+15=16分钟,此题答案为A。
二、购物选择问题
在购物选择问题中考生需要根据题干要求进行选择,最终使所花费资金最少。要是花费最少通常有两种考虑方式,一是正向考虑,选择花费最少的方式;二是反向考虑选择节省最多的方式。
例2、A、B两地分别有10台和6台型号相同的机器,准备配送到E、F两地,其中E地11台,F地5台。若每台机器从A到E和F的物流费用分别为350元和550元,从B到E和F的物流费用分别为600元和900元,则配送这16台机器的总物流费用最少为( )
A.7850元 B.8100元 C.8400元 D.8700元
解析:A地的运输费用都比B地来的低,此时我们就需要反向考虑,发现A到E比B到E可节省250元/台,而A到F比B到F可节省350元。要使物流费用最少就应该要节省最多,所以A地运送5台去F地,5台去E地,B地运送6台去E地,共用550×5 + 350×5 + 600×6 = 8100元。故此题答案为B。
总的来说,解决统筹问题的关键就在于要学会选择最优,在时间安排上要用时最少,所谓事半功倍,在资金花费上要消费最低,做到性价比最高。
行测答题技巧:解析数量关系中的交替合作问题
数量关系在各种公职类考试中多有涉及,题型分类繁多,变化灵活,但考试重点万变不离其宗,掌握核心考点即可在考试中帮助广大考生拿到必要的分数。行程问题作为常考考点,分为普通工程、多者合作、交替合作三种类型,其中以交替合作难度最高,最应该掌握。小编带您拨开迷雾——解析交替合作的技巧。
一、题型概述
其题型描述多为工程相关,但工作方式由普通的若干人合作完工,转换为每人轮流工作的交替合作问题。
【例】:甲乙两个工程队合作挖一条隧道,如果甲队单独施工要20天完成,乙队单独施工要10天完成。如果甲先挖一天,然后乙接替甲挖一天,再由甲接替乙挖一天……两人如此交替合作。那么,挖完这条隧道共要多少天?
A.13 B.13.5 C.14 D.15.5
【解析】读题可知,此题在多者合作基础上引入了循环问题,所以要结合工程常用的特值法,重点解决循环问题。
根据甲单独20天,乙10天,可设总工程量为20,则甲的效率为1,乙的效率为2。由于两人工作方式为甲乙、甲乙、甲乙……如此循环,每两天构成一个循环,直接求解天数不易求解,应先求出循环周期数,通过周期求天数。
每个周期的效率为:1+2=3,所以完成工作需要的周期数为20÷3=6……2,即六个完整的周期,还余下2个工作量。六个周期需要时间为12天,余下2个工作量:甲1天,剩下的1个工作量,乙还需0.5天即可完成。所以共12+1+0.5=13.5天,选择B。
二、巩固提高
【例】:一个工程,甲单独做需要12小时完成;乙单独做需要15小时完成。现在,甲乙两人轮流工作,按照甲2小时,乙1小时;甲1小时,乙2小时;甲2小时,乙1小时……如此交替下去,完成这件工作共需多长时间?
A.13小时 B.13小时20分钟
C.13小时12分钟 D.14小时
【解析】:C。根据甲和乙工作时间,可设工作总量为60,甲的效率为60÷12=5,乙的效率为60÷15=4,读题可知,最小循环周期为甲2小时,乙1小时,甲1小时,乙2小时,如此6小时一个循环,那么最小循环周期内的效率和为5×2+4+5+4×2=27,循环周期数为60÷27=2……6,两个循环周期对应12个小时,剩下6个工作量,甲接着做,每小时完成5,还需6÷5=1.2小时,即1小时12分钟。共需时间12小时+1小时12分钟=13个小时12分钟。
行测数量关系模拟题及答案
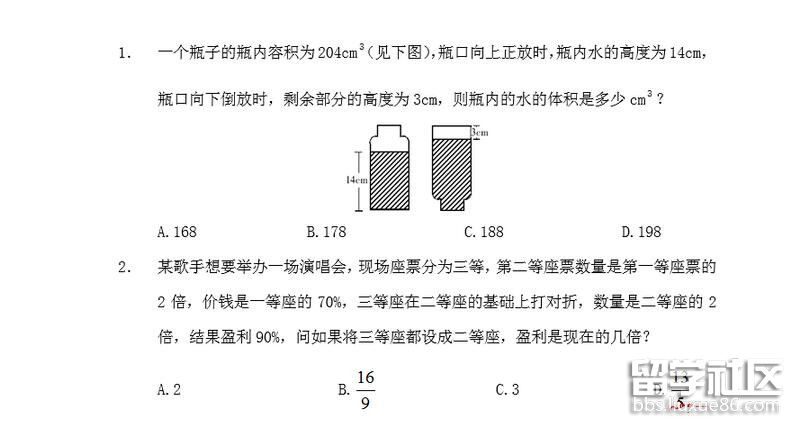
3. 甲、乙和丙三种不同浓度、不同规格的酒精溶液,单瓶重量分别为3公斤、7公斤和9公斤,如果将甲乙各一瓶、甲丙各一瓶和乙丙各一瓶分别混合,得到的酒精浓度分别为50%、50%和60%。如果将三种酒精各一瓶混合,得到的酒精中要加入多少公斤纯净水后,其浓度正好是50%?
A.1 B.1.3 C.1.6 D.1.9
【参考答案与解析】

来源:中公教育
小编精心为您推荐:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |