公务员行测组合数列有哪些答题技巧？想学习这块的朋友可以来看看，下面出国留学网小编为你准备了“公务员行测组合数列答题技巧”内容，仅供参考，祝大家在本站阅读愉快！
公务员行测组合数列答题技巧
在部分地区的行测考试会考查数字推理题，数字推理题的难度并不是特别高，绝大多数是比较常规的。常见的考试形式有：等差数列，和数列，倍数数列，多次方数列，分式数列，和组合数列。当然，数字推理里面有些题目也会出的比较灵活。但这种的题量占比不同。
今天主要针对其中的一类比较特殊的考点组合数列进行介绍。组合数列可以分成两种：1，长数列；2，数位组合数列。
长数列
常规的数字推理题一般情况下会有六个数字左右，但长数列与常规数列最大的不同在于数字个数较多，一般而言会达到八个及以上。
对于长数列我们最常采用的解题方式就是分组，而常用的分组形式有间隔分组和两两分组或者三三分组。所谓的间隔分组就是我们把八个数列当中的八个数字中第一个、第三个、第五个、第七个放到一起组成一个新的数列，把第二个、第四个、第六个、第八个放到一起组成一个新的数列，分别来找这两个新的数列的关系。而所谓的两两分组就是当有八个数字或者十个数字的时候我们可以两个数字放到一起分成四组或五组，找到他们拥有的相同的规律。当原数列有九个数字的时候我们可以相邻三个数字结合分成三个组，找他们所拥有的相同的规律。
数位组合数列
数位组合数列的特点是单个数字的位数比较多，与常规的数列相比。该数列当中的每一个数都可能是多位数。而对于这种数列我们可以采取分段的方式进行解决。
1、对于一个三位数，肯定是有百位、十位、个位共同组成的，那我们就可以把他们每个数字中的百位提取出来，十位提取出来，个位提取出列，组成三个新的数列，找他们相同位置上面各自的规律。
2、或者我们单独看每个数字内部个位、十位、百位上面是否存在一定的运算关系，比如236这个数字，我们可以认为百位×十位=个位。
3、还有就是每个数字各个位数相加的和看一下是不是一样的或者构成一个有规律的和。
【例题1】 2，3，4，9，8，27，16，81，32，，243，（ ）
A.64 B.128 C.486 D.729
【答案】A
【解析】题干数列有10项，非常典型的“长数列”。从数项变化的方向上来看，先变大又变小，符合“忽大忽小”的特征。这时候优先考虑“奇偶分组”，即奇数项为一组（2，4，8，16，32），倍数关系明显，为等比数列，公比为2，因此所求为64，选择A。
【例题2】 7，14，5，15，3，12，2，（ ）
A.4 B.10 C.5 D.6
【答案】B
【解析】观察题干，数项超过6项，非常规律的“忽大忽小”，但是这道题并不会直接考虑“奇偶分组”，而是考虑两两一组。为什么呢？这是因为相邻两项间存在明显的倍数关系。这时候应该先关注倍数关系，两两一组之后不难发现后项分别是前项的2倍，3倍，4倍，因此下一组应该是5倍，所求为2×5=10，选择B。
行测指导：用画图解扶梯问题
行程问题是行测中的常考考点，其中的一个考点---扶梯问题，对于很多同学而言，不太容易理解。其实，扶梯问题就是数学在生活中的应用最典型的例子之一。相信每一个同学都逛过商场，乘坐过扶梯，那其中到底蕴藏了什么样的数学知识呢？今天就带大家一起来学习一下。
一、扶梯问题基础知识
1、画图解流水行船问题
2、流水行船问题的等量关系
3、方程的解法
二、学习目标
1、对扶梯问题中顺（逆）理解以及速度理解
2、在扶梯问题的相遇与追及问题中引入方程
3、解决扶梯问题时通过画线段图帮助理解题目，并最终掌握通过公式解题
三、知识梳理
1、速度的单位不是我们常见的“千米每小时”、“米每秒”，而是“每分（秒）钟走多少个台阶”
2、在扶梯问题中“总路程”并不是求扶梯有多少“（千）米”，而是求扶梯的“静止时可见台阶总数”
3、方向一致，速度加和；方向相反，速度作差。根据路程构造等量关系，解方程即可
四、常见考点及典型例题
（一）已知时间
【例1】商场的自动扶梯以均匀的速度由下往上运行，两个孩子嫌扶梯走得太慢，于是在运行的扶梯上，男孩每秒向上走2个梯级，女孩儿每2秒向上走3梯级，结果男孩用40秒达到楼上，女孩用50秒到达。问当扶梯静止时，扶梯可看到的梯级共有多少级？
解析：题目中已知男孩和女孩的速度及分别所用时间，我们可以根据路程相等构造等量关系。男孩速度=2梯/秒，时间为40秒，时间女孩速度=1.5梯/秒，时间为50秒。
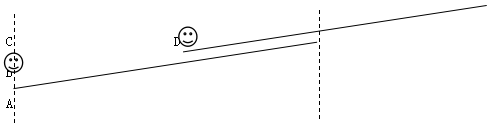
如图所示，如果男（女）孩静止不动，40（50）秒后就应该在B位置，正是由于扶梯的自动运行，才能够使得男（女）孩达到楼上。AB就是自动扶梯运行的距离，BC就是男（女）孩走的距离。设扶梯自动的运行的速度为V，由此可得：（2+v）×40=（1.5+v）×50，v=0.5级/秒。级数=2.5×40=2×50=100级。
小结：当行驶方向和自动扶梯的运行方向一致时，得到的结论和相遇问题的公式一致；路程和=速度和×时间。同理，当行驶方向和自动扶梯的运行方向不一致时，可运用路程差=速度差×时间的方式解题。只不过在扶梯问题中，此处的路程差与路程和皆为自动扶梯的级数。
（二）已知级数
【例2】哥哥沿向上移动的自动扶梯从上往下走，共走了100级；此时妹妹沿向上的自动扶梯从下往上走到顶，共走了50级。如果哥哥单位时间内走的级数是妹妹的2倍。那么，当自动扶梯静止时，自动扶梯能看到的部分有多少级？
解析：题目中已知哥哥和妹妹走的级数（路程）及速度关系，可通过假设速度的方式表示出时间。假设妹妹的速度为x，哥哥的速度为2x，可得哥哥所需时间
，妹妹所需时间
。假设扶梯速度为v，根据路程相同可得：
，可得v=0.5x，所求
。
行测数量关系排列组合理论基础讲解
在排列组合中，计数原理主要包括分类加法计数原理和分步乘法计数原理，如何正确选取两种计数原理是排列组合题的取胜之匙。
1.分类加法计数原理
对于分类加法计数原理，我们可以理解为对于完成某件事的不同方案，每个方案都相互独立，且都能直接达到这件事的最终目标，因此我们把所有的方案加起来。比如完成某件事有n类不同的方案，第1类方案有
种不同的方法，第2类方案有
种不同的方法，第3类方案有
种不同的方法，……，第n类方案有
种不同的方法，那么完成这件事共有
种不同的方法。
2.分步乘法计数原理
对于分步乘法计数原理，我们可以理解为对于完成某件事的不同步骤，每个步骤之间承上启下，只有所有步骤共同发挥作用，才算完成这件事，因此所有的步骤之间相乘。如完成某件事需要n个步骤，做第1步有种不同的方法，做第2步有种不同的方法，做第3步有种不同的方法，……，做第n步有种不同的方法，那么完成这件事共有
种不同的方法。
3.两种计数原理的区别
通过上述对两种计数原理的描述，在实际做题的过程中我们可以将题目的目标前置，判断不同的方案或步骤能否直接完成目标，如果能直接完成目标则选择分类加法计数原理，如果不能直接完成目标则选择分步乘法计数原理。
4.例题
【例题1】小明和小刚从4门不同的课程中各选修2门，则他俩所选的课程中恰有1门相同的选法有（ ）种。
A.6 B.12 C.24 D.30
【解析】根据题意两人所选课程只有一门课程相同，可以让两人从4门课程中先同选1门，有4种不同的选法；其次小明从剩下的3门课程中任选1门，有3种不同的选法；再让小刚从最后的2门课程中任选1门，有2种不同的选法。这道题中我们分步骤选择课程，根据描述可以判断为分步乘法计数原理，所以，小明和小刚所选的课程中恰有1门相同的选法共有4×3×2=24（种）。故本题选C。
【例题2】某超市为顾客提供四种结账方式：现金、支付宝、微信和信用卡。若顾客甲只会用现金结账，顾客乙只会用现金和信用卡结账，顾客丙与甲乙结账方式都不同，丁哪种方式都可以，若甲乙丙丁购物后依次结账，那么他们共有（ ）种结账方式的组合。
A.36种 B.30种 C.24种 D.20种
【解析】当乙用现金结算时，此时甲和乙都用现金结算，所以丙有3种结算方式，丁有4种结算方式，共有3×4=12（种）不同的结算方式；当乙用信用卡结算时，此时甲用现金结算，丙有2种结算方式，丁有4种结算方式，共有2×4=8（种）不同的结算方式。综上，共有12+8=20（种）不同的结算方式。故此题选D。
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |