数学对于很大一部分考生来说从小到大都是一个棘手的科目,这样的难题从中考其实就已经显现出难度了,以下内容是出国留学网为大家整理的"2022年深圳中考数学部分真题详细解析",不妨来感受一下现在的初中生做的数学题到底有多难!

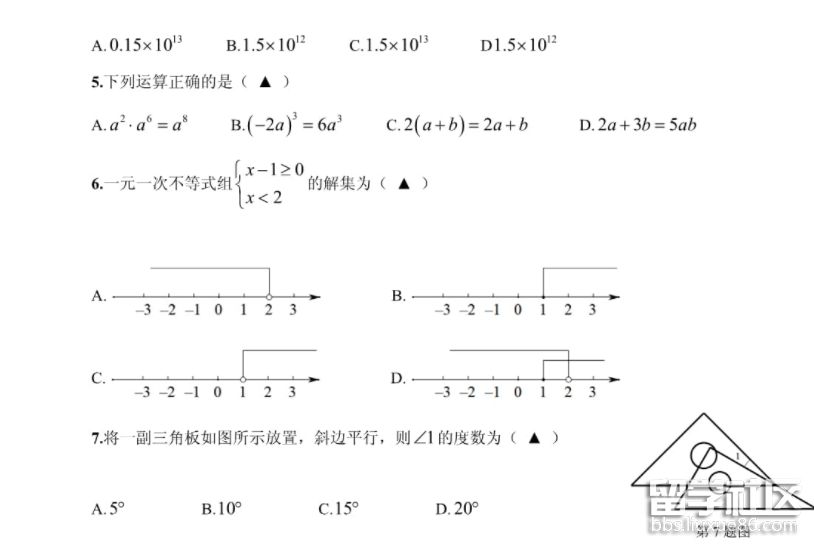

10.已知三角形ABE为直角三角形,∠ABE=90°,BC为圆的切线,C为切点,CA=CD,则ABC和CDE面积之比为( )
A.1:3 B.1:2 C.√2:2 D.(√2-1):1
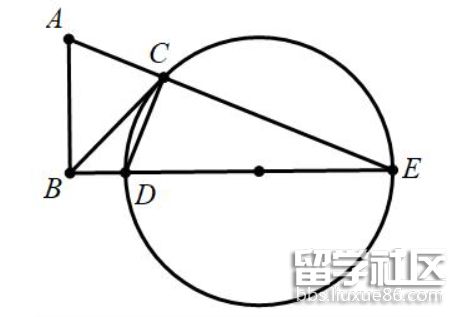

16.已知ABC是直角三角形,∠B=90°,AB=3,BC=5,AE=2,连接CE以CE为底作直角三角形CDE且CD=DE,F为AE边上的一点,连接BD和BF,且∠FBD=45°,则AF的长为______

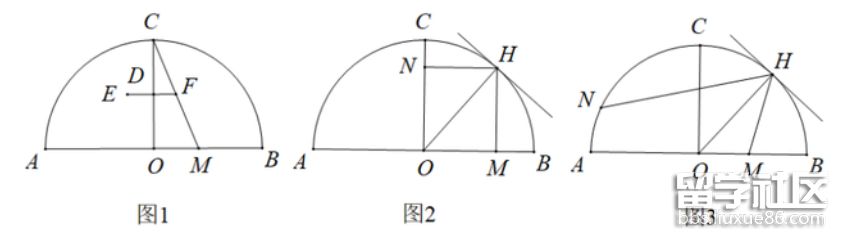
21.一个玻璃球体近似半圆O,AB为直径,半圆O上点C处有个吊灯EF,EF||AB,COAB,EF的中点为D,OA=4,
(1)如图,CM为一条拉线,M在OB上,OM=1.6,DF=0.6,求CD的长度.
(2)如图,一个玻璃镜与圆O相切,H为切点,M为OB上一点,MH为入射光线,NH为反射光线,∠OHM=∠HON=45°,求ON的长度.
(3)如图,M是线段OB上的动点,MH为入射光线,∠HOM=50°,HN为反射光线交圆O于点N,在M从O运动到B的过程中,求N点的运动路径长.

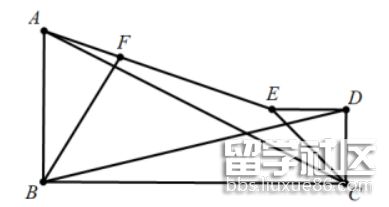
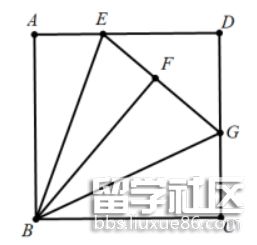
21.(1)发现:如图所示,在正方形ABCD中,E为AD边上一点,将AEB沿BE翻折至BEF处,延长EF交CD于点G,求证:BFEBCG;
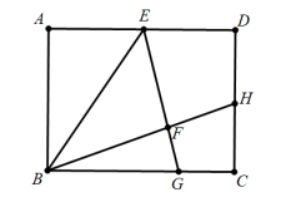
(2)探究:如图,在矩形ABCD中,E为AD边上一点,且AD=8,AB=6,将AEB沿BE翻折至BEF处,延长EF交BC于点G,延长BF交CD于点H,且FH=CH,求AE的长;
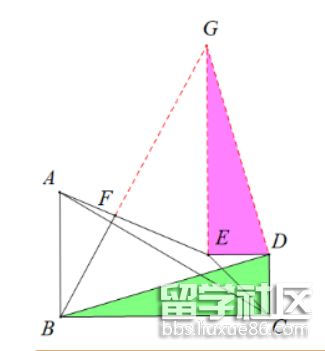
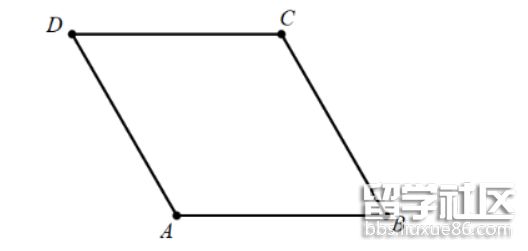
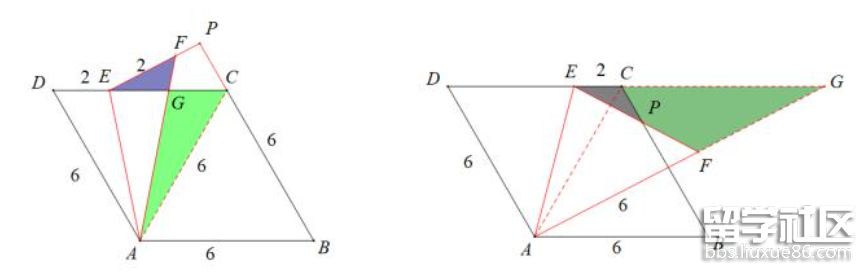
(3)拓展:如图,在菱形ABCD中,E为CD边上的三等分点,∠D=60°,将ADE沿AE翻折至AFE,直线EF交BC于点P,求PC的长.
解:(1)HL可证明;比较简单,交给同学们自己证明;
(2)

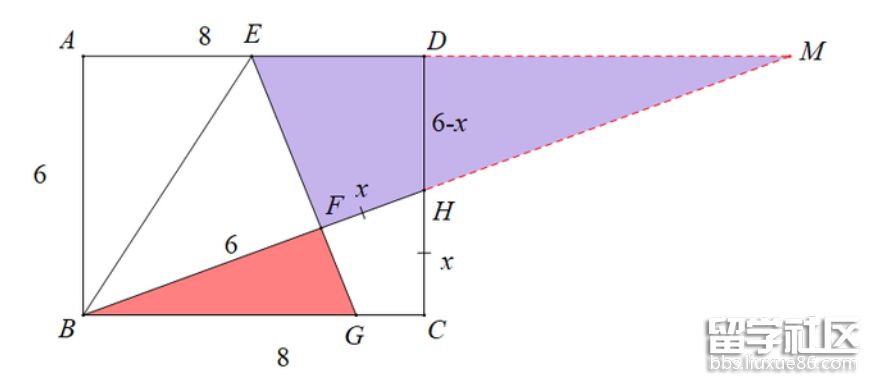

点评:选择压轴题,比较新颖,可能部分同学不太适应,与平时练习的题目风格还是有差异,当然实际难度并没有想象中的大;填空压轴题,手拉手模型,看答案挺简洁的,但是在考场上,有多少同学能在短时间内想到呢,这得打个问号;
解答题压轴,仍以几何为主,对同学们确实有一定的挑战,毕竟以后总是考二次函数压轴,而2021、2022都考察几何;21题难度常规,题型也是同学们少见的圆中的路径长;
22题,第3问的难度就体现区分度了,画图和辅助线是难点;找多次相似,对基础弱的同学而言几乎不可能了,而对于基础好的,也要看考场的发挥状态.
推荐阅读:
| 语文真题 | 数学真题 | 英语真题 | 物理真题 | 化学真题 | 历史真题 | 政治真题 |
| 语文答案 | 数学答案 | 英语答案 | 物理答案 | 化学答案 | 历史答案 | 政治答案 |