二次根式化简的基本方法
湖北省黄石市下陆中学 陈 勇
二次根式是中学代数的重要内容之一,而二次根式的化简是二次根式运算的基础,学好二次根式的化简是学好二次根式的关键。下面给同学们归纳总结了几种方法,帮助大家学好二次根。
一、乘法公式法
例1 计算:![]()
解:原式=![]()
![]()
=![]() ×
×
=19![]()
二、因式分解法
例2 化简: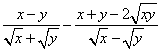 。
。
分析:该题的常规做法是先进行分母有理化,然后再计算,可惜运算量太大,不宜采取。但我们发现(x-y)和(x+y-
解:原式=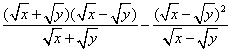
=![]()
=0.
三、整体代换法
例3 化简![]() 。
。
解:原式=![]()
=![]()
=![]()
=![]()
=4x+2
四、巧构常值代入法
例4 已知![]() ,求
,求![]() 的值。
的值。
原式=![]() =
=![]() =2.
=2.
以上就是二次根式化简的一些方法,希望同学们在学习中活学活用,并能总结出更多更好的计算方法来。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |


