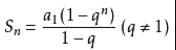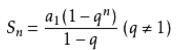数学方面有公式计算可能朋友们都不知道是怎样的,比如我们常说的等比数列求和公式,今天出国留学网小编就带大家来了解下这方面的详细内容,想深入了解的朋友可以参考下。
等比数列求和公式是怎样的
公式:q≠1时 Sn=a1(1-q^n)/(1-q)=(a1-anq)/(1-q)q=1时,Sn=na1。
1.等比数列求和公式是求等比数列之和的公式。如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,常用G、P表示,这个常数叫做等比数列的公比。
2.数列是函数概念的继续和延伸,是定义在自然集或它的子集{1,2,…,n}上的函数。对于等差数列而言,可以把它看作自然数n的“一次函数”,前n项和是自然数n的“二次函数”。等比数列可看作自然数n的“指数函数”。
3.形如y=a^x(a>0且a≠1) (x∈R)的函数叫作指数函数。也就是说以指数为自变量,底数为大于0且不等于1的常量的函数称为指数函数,它是初等函数中的一种。它是定义在实数域上的单调、下凸、无上界的可微正值函数。 数学术语指数函数是数学中重要的函数。
上述文章就是出国留学网小编要给大家分享的内容了,希望朋友们看完等比数列求和公式是怎样的后都能完全理解。关注我们,每天更新不一样的文章知识点。
推荐阅读:
...