想要高考取得好的成绩,高中的复习是至关重要的,在这里,出国留学网小编为大家整理了高中数学知识点总结,希望能够帮各位高三学生更好的复习,如果觉得本网站内容有用,欢迎收藏(Ctrl+D即可)。
【解析几何】

1、直线
两点距离、定比分点 直线方程
|AB|=| |
|P1P2|=
y-y1=k(x-x1)
y=kx+b
两直线的位置关系 夹角和距离
或k1=k2,且b1≠b2
l1与l2重合
或k1=k2且b1=b2
l1与l2相交
或k1≠k2
l2⊥l2
或k1k2=-1 l1到l2的角
l1与l2的夹角
点到直线的距离
2.圆锥曲线
【圆 椭 圆】
标准方程(x-a)2+(y-b)2=r2
圆心为(a,b),半径为R
一般方程x2+y2+Dx+Ey+F=0
其中圆心为( ),
半径r
(1)用圆心到直线的距离d和圆的半径r判断或用判别式判断直线与圆的位置关系
(2)两圆的位置关系用圆心距d与半径和与差判断 椭圆
焦点F1(-c,0),F2(c,0)
(b2=a2-c2)
离心率
准线方程
焦半径|MF1|=a+ex0,|MF2|=a-ex0
双曲线 抛物线
双曲线
焦点F1(-c,0),F2(c,0)
(a,b>0,b2=c2-a2)
离心率
准线方程
焦半径|MF1|=ex0+a,|MF2|=ex0-a 抛物线y2=2px(p>0)
焦点F
准线方程
坐标轴的平移
这里(h,k)是新坐标系的原点在原坐标系中的坐标。
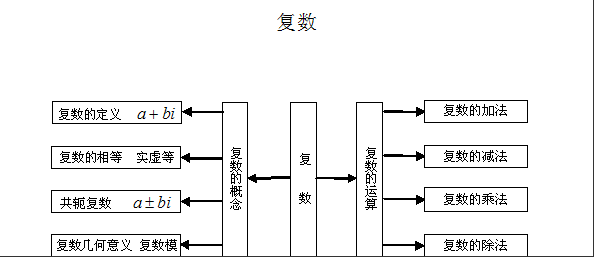
【复数】

代数形式 三角形式
a+...

