行测数量的运算一直是行测考试的重点题型,下面由出国留学网小编为你精心准备了“行测技巧:两种方法巧解数量关系“容斥问题””,持续关注本站将可以持续获取更多的考试资讯!
行测技巧:两种方法巧解数量关系“容斥问题”
容斥问题其实是一种在考试中比较常见且简单的题型,它考察的是集合之间彼此的交集问题,一般来说解决容斥问题最常用的两种方法就是文氏图法和公式法。下面小编为大家讲解。
让我们先从一个生活上的小例子来理解什么是容斥:AB是两个同居室友,有一天A下班回家时在路上买了香蕉、苹果、菠萝三种水果,B回家路上买了菠萝、葡萄、西瓜三种水果,那么家里现在一共有多少种水果?答案很简单,因为尽管两个人各买了三种水果,但其中菠萝是重复的,所以我们在3+3之后还需要把多算了一遍的菠萝减下去,而这就是容斥问题的本质:减去多算的,补上空白的。
在行测的容斥问题里,较常考的是三者容斥,也就是三个集合之间的关系,我们把三个集合分别称作A、B、C,三个集合的总集称作U,就可以得到三者容斥的公式:
U=A+B+C-A∩B-B∩C-A∩C+A∩B∩C+三者都没有的
在做题的时候只需要找到题干中给定的各个条件,选择直接套用,然后就可以求出公式中缺少的项,从而快速得到答案。
以一道题目为例:18名游泳运动员中,有8名参加仰泳,有10名参加蛙泳,有12名参加自由泳,有4名既参加仰泳又参加蛙泳,有6名既参加蛙泳又参加自由泳,有5名既参加仰泳又参加自由泳,有两名这三个项目都参加。三个项目都没有参加的有多少名?
在题目中,ABC即对应仰泳、蛙泳、自由泳,那么A、B、C、A∩B,B∩C,A∩B∩C都是已知的,求都没有参加,即求剩下的项,首先,我们先把题目中已经给的数据填入公式:
18=8+10+12-4-6-2+2+x
在这个方程中,我们解得x=1,也就是三个项目都没有参加的有一个人。
而公式法虽然简单,但有的时候可能会觉得有些眼花缭乱,这种时候文氏图法就显得更为直观,我们一起来感受一下文氏图法在题目中的应用:
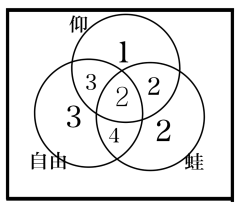
按照从内向外依次填充的方式,在文氏图中填写不同区域对应的数据,这样题目无论是求哪个部分,又或是其中一些部分的和、差关系(比如只会游一种泳的、只会游两种泳的、只会自由泳的人比只会蛙泳的多多少),我们就都不怕了。
所以,公式法简洁,文氏图灵活,两种方法各有千秋,大家可以根据题目的特点灵活运用,从而在考试中将容斥问题快速解决。
推荐阅读: