第三部分 数量关系
(共10题,每题1.5分,共15分,参考时限15分钟)
在这部分试题中,每道题呈现一段表述数字关系的文字,要求你迅速、准确地计算出答案。
请开始答题:
56、某单位利用业余时间举行了3次义务劳动,总计有112人次参加。在参加义务劳动的人 中,只参加1次、参加2次和3次全部参加的人数之比为5:4:1。问该单位共有多少人参加了义务劳动?
A.70 B.80
C..85 D.102
56.A【解析】和差倍比问题。由于参加人数之比为5:4:1,则对应人次之比为5:8:3,对应的总人次为112,所以参加1、2、3次的人次分别为35、56、21,对应人数分别为35、28、7,故总人数为70人。因此,答案选择A选项。
57、某工厂有100名工人报名参加了4项专业技能课程中的一项或多项,已知A课程与B课程不能同时报名。如果按照报名参加的课程对工人进行分组,将报名参加的课程完全一样的工人分到同一组中,则人数最多的组最少有多少人?
A.7 B.8
C..9 D.10
57.D【解析】排列组合结合最值问题。考虑不同的选择方法,可选1、2、3种课程,总共为4+5+2=11种。设人数最多的组最少有x人,其余各组亦均为x人,11x=100,x=100/11,故x的最小值为10.因此,答案选择D选项。
58、某单位组织参加理论学学的党员和入党积极分子进行分组讨论,如果每组分配7名党员和3名入党积极分子,刚还剩下4名党员未安排;如果每组分配5名党员和2名入党积极分子,则还剩下2名党员未安排,问参加理论学习的党员比入党积极分子多多少人?
A.16 B.20
C.24 D.28
58.B【解析】由题意,总人数除以10余数为4,总人数除以7余数为2,故满足要求的总人数最小为44,代入验证可得共32名党员和12名入党积极分子。相差20人。因此,答案选择B选项。
59、环形跑道长400米,老张、小王、小刘从同一地点同向出发,围绕跑到分别慢走、跑步和骑自行车。已知三人的速度分别是1米/秒、3米/秒和6米/秒,问小王第3次超越老张时,小刘已经超越了小王多少次?
A.3 B.4
C.5 D.6
59.B【解析】行程问题,环形多次追及。由路程差=速度差×时间,可得1200=(3-1)×t,解得t=600秒。再由上述公式可解得小刘与小王的路程差=(6-3)×600=1800米,即4圈。因此,答案选择B选项。(另外,本题可直接由比例法求解:速度差之比为3:2,所以路程差之比亦为3:2,故小刘比小王多跑了4.5圈。)
60、甲乙两辆车从A地驶往90公里外的B地,两车的速度为5:6。甲车于上午10点半出发,乙车于10点40分出发,最终乙车比甲车早2分钟到达乙地。问两车的时速相差多少千米/小时?
A.10 B.12
C.12.5 D.15
60.D【解析】行程问题。比例法求解。由于两人的速度之比为5:6。故两人所用时间之比为6:5,设甲用时为x,则乙用时为x-12。x:(x-12)=6:5,解得x=72分钟。所以甲、乙两人的速度分别为75和90,相差15千米/小时。因此,答案选择D选项。
61、药厂使用电动研磨器将一批晒干的中药磨成药粉。厂长决定从上午10点凯斯,增加若干台手工研磨器进行辅助作业。他估算如果增加2台,可在晚上8点完成,如果增加8台,可在下午6点完成。问如果希望在下午3点完成,需要增加多少台手工研磨器?
A.20 B.24
C.26 D.32
61.C【解析】牛吃草问题。代入公式y=(N-x)×T,可得y=(2+x)×10,y=(8+x)×8;解得y=240,x=22。所以240=(N+22)×5,解得N=26。因此,答案选择C选项。
62、箱子里有大小相同的3种颜色玻璃珠各若干颗,每次从中摸出3颗为一组,问至少要摸出多少组,才能保证至少有2组玻璃珠的颜色组合是一样的?
A.11 B.15
C..18 D.21
62.A【解析】排列组合结合最值问题。首先计算所有不同的分组情况:三个小互不相同,共1种情况;三个小球颜色相同,共3种情况;三个小球为两种颜色,共
=6种。故不同的分组方式共10种,为了保证至少有两组玻璃珠的颜色组合一样,共需摸出10+1=11组玻璃球。因此,答案选择A选项。
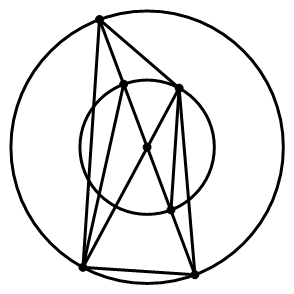
63、一个圆形的草地中央有一个与之同心的圆形花坛,在花坛圆周和草地圆周上各有3个不同的点,安放了洒水的喷头,现用直管将这些喷头连上,要求任意两个喷头都能被一根水管连通,问最少需要几根水管?(一根水管上可以连接多个喷头)
A.5 B.8
C..20 D.30
63.B【解析】几何构造。如下图所示,先让四点(喷头)共线,再让剩余的两个点与之前其中一点三点共线,共需8段水管。
64、某市电价为一个自然月在100度以内的每度电0.5元,在101度到200度之间每度电1元,在201度以上的每度电2元。张先生家第三季度缴纳电费370元,该季度用电最多的月份用电量不超过用电最少月份的2倍,问他第三季度最少用了多少度电/
A.300 B.420
C..480 D.512
64.C【解析】分段计费问题。代入排除。居中代入C项。设最少的两个月份用电为x度、则最多的2x度。居中代入C项480。解得x=120。代入计算电费可得恰为370元。因此,答案选择C选项。
65、某有色金属公司四种主要有色金属总产量的1/5为铝,1/3为铜,镍的产量是铜和铝产量之和的1/4,而铅的产量比铝多600吨,问该公司镍的产量为多少吨?
A.800 B.600
C.1000 D.1200
65.B【解析】和差倍比问题。设总产量为15份,由题意,其中铝为3份,铜为5份,镍为2份,铅为5份,故铅比铝多2份为600吨。所以镍为600吨。因此,答案选择B选项。
| 行测真题 | 行测答案 | 申论真题 | 申论答案 | 面试专题 |