行测数量关系：比较构造法解决方程问题

　　今天小编为大家提供行测数量关系：比较构造法解决方程问题，希望大家好好掌握本文中提到的方法，提高答题速度！祝你备考顺利！

　　行测数量关系：比较构造法解决方程问题

　　行测方程问题是考生相对来说都比较熟悉的一部分内容，而且大部分考生也喜欢用方程法去解题。小编认为，普通的等量构造法涉及程序比较复杂，这就导致解题时间较长，在实际考试过程中没有时间去做。而比较构造就能够避过中间的设、列阶段，直接进入解方程，大大的节省了解题时间，提高做题效率。

　　一、什么是比较构造法

　　对同一事件有两种或两种以上不同方案，比较方案间的异同，建立方案间的联系，构造关系式，这就是比较构造法。

　　二、一般解题步骤

　　1、列出方案

　　2、比较方案间差别与联系

　　3、构造关系式

　　4、求解

　　三、应用

　　例1：将一堆苹果放进一些筐，如果每筐放12个，则多出3个苹果放不下，如果每筐放14个苹果，则又缺5个苹果，总共有多少个苹果?

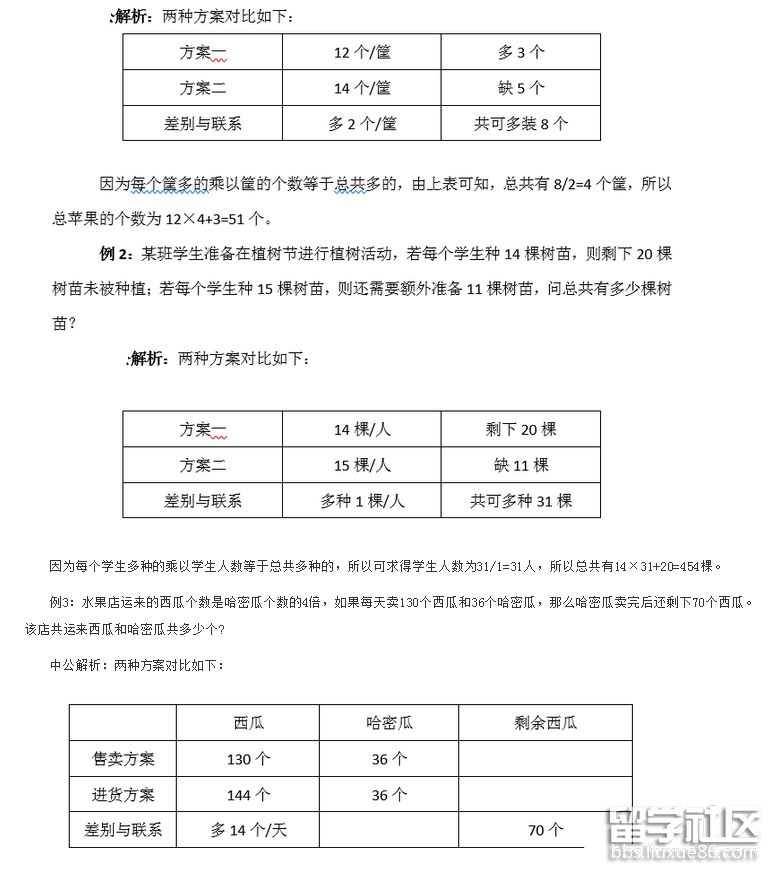
　　比较售卖方案和进货方案，因为每天卖出36个哈密瓜，哈密瓜全部卖完，而剩余了70个西瓜，假设每天进36个哈密瓜，因为西瓜的进货量是哈密瓜的4倍，所以每天进144个西瓜，每天剩余西瓜数为14个，共剩余70个，可得售卖天数为70/14=5天。所以，该店共运来西瓜和哈密瓜共(144+36)×5=900个。

　　其实比较构造法并不难。考生要多应用这种方法，尽量不去列方程，用思考代替计算，可以大大降低计算量，提高做题速度，提高正确率。

　　行测数量关系：等差数列

　　在行测考试过程中，数量关系成为了我们考生很头疼的一部分内容。去做吧，感觉很耗时间;不去做吧，分值又很大。所以考生必须具备一定的能力去快速的解决这些问题。当然，拥有特殊性质和运算技巧的等差数列成为了行测考试的一个热门，非常受命题人的青睐。接下来小编跟大家一起来快速的学习一下等差数列在考试中的运用。

　　一.什么是等差数列

　　等差数列：如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差常用字母d表示。

　　二.考生需掌握的核心：