在初一上学期,我们学习了整式的加减. 就如同在学习数的运算一样,加减法之后学习乘除法,本章就是继整式的加减法之后,进一步研究了关于整式的第二级运算——整式的乘除.
一、知识要点
对于本章知识的学习,应达到以下要求:
1、掌握幂的运算性质,会用它们进行运算;
2、掌握单项式运算以及多项式运算的法则,会用它们进行运算;
3、灵活运用乘法公式,熟练使用它们解题;
4、会进行整式的加、减、乘、除、单项式的乘方等混合运算;灵活使用运算律与各种公式进行简便运算.
二、知识结构
在本章所有的知识中,幂的运算性质是最基础的,它是单项式乘除法、多项式乘除法以及使用乘法公式运算的必备知识;其中,单项式乘除法又是多项式乘除法运算的知识基础. 它们之间的关系可有下面的知识结构图来表示:
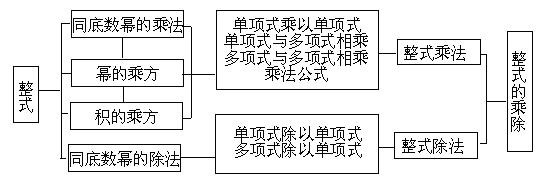
三、基础知识
学习本章包括幂的运算性质、单项式乘除法、多项式乘除法、乘法公式四部分内容. 其中,乘法公式是重点.
1、幂的运算性质包括:
(1) 同底数幂的乘法:am·an=am+n(m,n为正整数);
(2) 幂的乘方:(am)n=amn(m,n为正整数);
(3) 积的乘方:(ab)n=an·bn(n为正整数);
(4) 同底数幂的除法:am÷an=am-n(a≠0, m,n为正整数,并且m>n).
2、单项式乘除法主要指两种运算:
(1) 单项式乘以单项式;
(2) 单项式除以单项式.
3、多项式乘除法学习了三种运算:
(1) 单项式与多项式相乘;
(2) 多项式与多项式相乘;
(3) 多项式除以单项式.
4、本章中介绍了两种(三个)乘法公式:
(1) 平方差公式:(a+b)(a-b)=a2-b2;
(2) 完全平方公式:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.
需要说明的是,有很多内容是通过本章知识派生出的,对于它们也应充分注意,比如:
1、在多项式乘法中,通过实例得出了:含有一个相同字母的两个一次二项式相乘,得到的积是同一个字母的二次三项式. 如果用a,b分别表示含有一个系数是1的相同字母的两个一次二项式中的常数项,则有公式:
(x+a)(x+b)=x2+(a+b)x+ab (*).
这个公式对于解此类多项式乘法的计算题,是非常有效的.
2、根据同底数幂除法的运算性质am÷an=am-n(a≠0, m,n为正整数,并且m>n),当指数相同时,则有an÷an=an-n =a0=1,从而诠释了“任何不等于0的数的0次幂都等于1”的道理,同时,又将同底数幂除法的运算性质中m>n的条件扩大为m≥n;而当m
3、同底数幂的乘法与除法性质的出现,进一步补充和完善了科学记数法的使用. 尤其是负指数幂的应用,使表示微观世界的物体特征变得简便易行.
四、思想方法
1、转化的数学思想方法:我们可以用转化思想来寻求平方差公式、完全平方公式以及公式(*)之间的关系. 对于公式(*)而言,当b= -a时,则有:
(x+a)(x-a)=x2+(a-a)x+a(-a)=x2-a2
此即平方差公式;当b=a时,(x+a)(x+a)=x2+(a+a)x+a·a,即
(x+a)2=x2+2ax+a2
此即完全平方公式.
若以和的完全平方公式(a+b)2=a2+2ab+b2为原型,当把b改为- b时,公式变为:
(a-b)2=a2+2a(-b)+(-b)2=a2-2ab+b2
此即差的完全平方公式.
在这些变形中,我们能很好的认识到事物在特定条件下可以相互转化的辩证关系,从而把不同的知识内容统一起来.
2、“特殊——一般——特殊”的思想方法:课本中,很多知识的得出,都是先举出一些具体的例子,然后找出它们的共同特征,加以推广,概括出一般化的结论,再把所得结论应用于具体的解题过程中。比如,在学习同底数幂的乘法时,教材先以两个具体的例子,作为出发点:
根据乘方的意义,得
103×102=(10×10×10)(10×10)=10×10×10×10×10=105;
23×22=(2×2×2)(2×2)=2×2×2×2×2=25.
由此总结出
103×102 =103+2;23×22=23+2.
若用字母a表示任意底数,则有
a3·a2 =(aaa)(aa)=aaaaa=a5.
也就是
a3·a2 =a5.
进一步推广,用字母m, n表示任意正整数,那么
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |