分式的意义和性质
一、分式的概念
1、用A、B表示两个整式,A÷
B可以表示成 2、既然除式里含有字母的有理代数式叫做分式,那么,在分式里分母所包含的字母,就不一定可以取任意值。分式 ![]() 的分子A可取任意数值,但分母B不能为零,因为用零做除数没有意义。一般地说,在一个分式里,分子中的字母可取任意数值,但分母中的字母,只能取不使分母等于零的值。
的分子A可取任意数值,但分母B不能为零,因为用零做除数没有意义。一般地说,在一个分式里,分子中的字母可取任意数值,但分母中的字母,只能取不使分母等于零的值。
3、(1)分式: ![]() ,当B=0时,分式无意义。
,当B=0时,分式无意义。
(2)分式:
(3)分式: ![]()
(4)分式: ![]() ,当
,当 ![]() 时,分式的值为
时,分式的值为
(5)分式: ![]() ,当
,当 ![]() 时,即
时,即 ![]() 或
或
(6)分式: ![]()
(7)分式: ![]() ,当
,当 ![]() 时 或
时 或 ![]()
二、分式的基本性质:
1、学习分式的基本性质应该与分数的基本性质类比。不同点在于同乘以或同除以同一个不等于零的整式,这个整式可以是数也可以是字母,只要是不为零的整式。
2、这个性质可用式子表示为:3、学习基本性质应注意几点:
(1)分子与分母同乘或同除的整式的值不能为零;(2)易范错误是只乘(或只除)分母或只乘(或只除)分子;
(3)如果分子或分母是多项式时,必须乘以多项式的每一项。
4、分式变号法则的依据是分式的基本性质。5、分式的分子,分母和分式的符号,改变其中任何两个,分式的值不变,如下列式子:
![]() ,
,
三、约分:
1、约分是约去分子、分母中的公因式。就是用分式中分子和分母的公因式去除分子和分母,使分式化简为最简分式,最简分式又叫既约分式。
2、约分的理论依据是分式的基本性质。
3、约分的方法:
(1)如果分式的分子和分母都是几个因式乘积的形式,就约去分子和分母中相同因式的最低次幂,当分子和分母的系数是整数时,还要约去它们的最大公约数。
四、例题分析
例1,请说出下列各式中哪些是整式,那些是分式?(1)
(4)
解:根据分式定义知(1)、(2)、(3)是分式,(
4)、(5)、(6)是整式。 说明:判断一个代数式是否是分式要紧紧抓住除式中含不含字母。
这里 ![]() 是分式,不能因为
是分式,不能因为
而认为
要区分分式的值和分式这两个不同的概念。
另外
虽然分母中有π,但π不是字母而是无理数,是无限不循环小数,因此
例2,在分式(1) ![]() (2)
(2) ![]()
解:(1)在 ![]()
(2)在 ![]() 中,当x=-2
中,当x=-2
(3)在 ![]() 中,当x=-2或
中,当x=-2或
∴x≠-2且x≠3。
例3,x为何值时,分式 解:(1)∵当分母2x+3=0时分式无意义,∴x=- ![]() 时,分式无意义。
时,分式无意义。
(2)∵当 ![]()
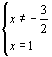 ,∴x=1时分式值为零。
,∴x=1时分式值为零。 (3)∵当 ![]()
(4)∵当 ![]() 或
或
∴ 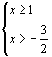 或
或 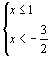 ∴ x≥1
∴ x≥1
例4,当x取何值时,分式 ![]() (1)值为零;(2
(1)值为零;(2
解:(1)∵当(x+3)(x-1)≠0时,分式有意义,∴当x≠-3且x≠1
时分式有意义。又∵6-2|x|=0时分式值为零,则3-|x|=0, ∴|x|=3, ∴x=±3。
∴
解:(2)∵(x+3)(x-1)=0分式无意义,
即
x+3=0或x-1=0,∴x=-3或x=1时分式无意义。说明:对于(1)也可先令分子为零,求出字母的所有可能值为x=±3后,再逐一代入分母验证是否为零,不为零者即为所求。
对于(2)当x+3=0或x-1=0时,都会使分式的分母等于零,所以要注意“或”字的使用。
解:(3)∵(x+3)(x-1)≠0
时分式有意义。即x+3≠0且x-1≠0时,∴x≠-3且x≠
1时分式有意义,说明:对于(3)分母(x+3)(x-1)只有不为零时,分式有意义,而(x+3)(x-1)≠0,当x+3=0或x-1=0都会使(x+3)(x-1)=0
,所以应将x=-3和x=1都同时排除掉,写成x≠-3且x≠1,用“且”字,而不用“或”字。意义为x不能为-3而且还不能为1,即-3和1都不能取。因为取任何其中一个值,分母(x+3)(x-1)都会为0,而使分式都会无意义。例5,写出等式中未知的分子或分母:
(1
)(1)分析:这类问题要从已知条件入手,根据分式的基本性质,分析变化的过程,如(1)右边分母x2-y2是(x+y)(x-y),而左边分母为x+y,所以需将左式的分子和分母同乘以(x-y)。
解:
(2)分析:左边分子a2-ab=a(a-b),而右边分子是a-b,所以需将左式的分子和分母同除以a。
解:(3)∵a2+ab=a(a+b)
(将分子因式分解) ∴ ![]() (比较分子,发现分子、分母同乘以a)
(比较分子,发现分子、分母同乘以a)
= ![]() ,2ab
,2ab
例6,把下列分式的分子和分母中各项的系数都化为整数。
(1) 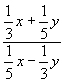 ; (2)
; (2) ![]()
(1)分析:先找到分式中分子和分母中的分母的最小公倍数为15,再据分数基本性质,分子和分母同乘以15。
解: 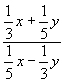 =
= 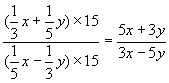
(2)解: ![]() =
= ![]() =
= ![]()
注:必须乘以分子和分母的每一项,避免发生(0.2a+3b)
×10=2a+3b这样的错误。 例7,不改变分式的值,使下列分式中分子与分母不含“-”号,(1)- ![]() ;(2)-
;(2)-
解:根据分式的符号法则得:
(1)- ![]() =
= ![]() ; (2
; (2
注意:分式、分子和分母的符号中,任意改变其中两个,分式的值不变。(1)中改变分式本身和分母两个负号,(2)中改变分子和分母两个负号。
例8,不改变分式的值,依照x的降幂排列,使分子和分母中x的最高项的系数都为正数。 (1) ![]() ;(2)
;(2)
解:(1) ![]() =
= ![]() =
= ![]() =
= ![]()
(2)- ![]() =-
=- ![]() =-
=- ![]() =-
=- ![]() 。
。
注意:如果分子或分母的首项为负,则必须先将负号提到括号外面,再使用符号法则,要注意避免下列的错误:
![]() =
= ![]() 。
。
例9,约分:(1) ![]()
解:(1) ![]() =
= ![]() =
=
注意:分母的因式约去后得1,分式变为整式。若化简分式 ![]() 时千万不要犯下列错误:
时千万不要犯下列错误:
![]() =
=
(2) ![]() =
= ![]() =
= ![]() =-
=- ![]() 。
。
注意:分母的负号一般要移去。
(2)如果分式的分子或分母是多项式,应先分解因式,然后再约分。
例10、约分:(1) ![]()
(3)
解:(1) ![]() =
=
注意:不要把 ![]() 约成
约成 ![]() =
= ![]() ,也不要将最后结果写成
,也不要将最后结果写成
(2) ![]() =
= ![]() 。
。
注:不要将 ![]() 约做
约做 ![]() ,因为这样是分子分母都减a2,不是同除以相同的整式。
,因为这样是分子分母都减a2,不是同除以相同的整式。
(
3) 注:不要犯下面的错误: ![]() =x3-x2
=x3-x2
(4) ![]() =
= ![]() =
= ![]()
= ![]() =-
=-
注意:这里应用到了(2-x)3=-(x-2)3的变形。
(5) ![]() =
= ![]()
= ![]() (分子提取公因式-1)
(分子提取公因式-1)
= ![]() (分子、分母都分解因式)
(分子、分母都分解因式)
=- ![]() (应用分式的符号法则)
(应用分式的符号法则)
说明:此题的解法,一方面显示出分式约分的一般步骤,另一方面在解题的右侧的括号内写出运算的算理,平日的化简是不写这些的,但不是它不存在,在思维上它是不可缺少的。
分数的乘除法的关键是约分,而分式乘除法的关键也是约分,就是说,分式乘除法运算的实质是约分,它能使运算的结果化为最简分式。同分数的约分一样,分式的约分是应用分式的基本性质,把分式的分子、分母同除以它们的公因式,把分式化简,因此约分的关键在于正确寻找到分式分子、分母中的公因式。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |


