造桥选址问题的拓展
湖北省黄石市下陆中学 宋毓彬
利用平移变换进行造桥选址,是平移变换的一个重要应用。下面就课本中一道习题,加以拓展探究,我们可发现其一般规律。
一、原题再现
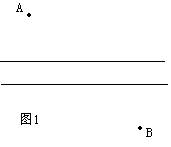
如图1,A和B两地在一条河的两岸,现要在河上造一座桥MN。桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)。(人教课标七年级下册2007年第二版37页第7题)
分析:由于河岸宽度是固定的,造的桥要与河垂直,因此路径AMNB中的MN的长度是固定的。
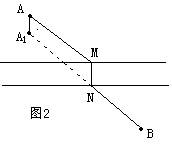
我们可以将点A沿与河垂直的方向平移MN的距离到A1,那么为了使AMNB最短,只需A1B最短。根据两点之间距离最短,连接A1B,交河岸于点N,在此处造桥MN,所得路径AMNB就是最短路径。如图2。
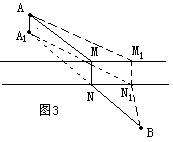
证明:如图3,如果在不同于MN的位置造桥M1N1。由于M1N1=MN=AA1;又根据“两点之间,线段最短”。可知,AN1+N1B>A1N+NB。
所以,路径AMNB要短于AM1N1B。
二、拓展应用
拓展1:如图4,如果A、B两地之间有两条平行的河,我们要建的桥都是与河岸垂直的。我们如何找到这个最短的距离呢?
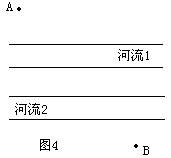
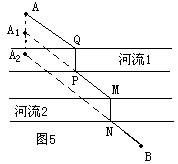
方法1:仿照上例,可以将点A沿与河垂直的方向平移两个河宽分别到到A1、A2,路径中两座桥的长度是固定的。为了使路径最短,只要A2B最短。连接A2B,交河流2河岸于N,在此处造桥MN;连接A1M,交河流1河岸于P,在此处造桥PQ。所得路径AQPMNB最短。
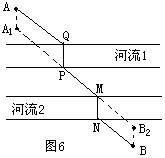
方法2:此题还可以用以下方法来确定建桥位置。
如图6,将点A沿与第一条河流垂直的方向平移一个河宽到A
1,将B沿与第二条河垂直的方向平移一个河宽到B1,连接A1B1与两条河分别相交于N、P,在N、P两处,分别建桥MN、PQ,所得路径AQPMNB最短。
拓展2:如图7,如果A、B之间有三条平行的河流呢?

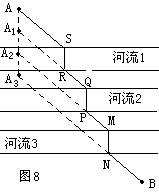
方法1:仿照拓展二方法1,将点A沿与河垂直的方向平移S三个河宽分别到到A1、A2、A3,路径中三座桥的长度是固定的。为了使路径最短,只要A
3B最短。
连接A3B,交河流3于N,在此处造桥MN;连接A2N,交河流2于P,在此处造桥PQ;连接A1Q,交河流1于R,在此处造桥RS。所得路径ASRQPMNB最短。
方法2:此处还可以先将A沿与河流1河岸垂直的方向平移两个单位到A1、A2,再将B沿与河流3河岸垂直的方向平移一个河宽到B1;或先将A沿与河岸垂直的方向平移1个单位到A1,再将B沿与河岸平移2一个河宽到B1、B2,来选择修桥位置。(请同学们自己画出图形。)
拓展3:如图
9,如果在上述条件不变的情况下,两条河不平行,又该如何建桥?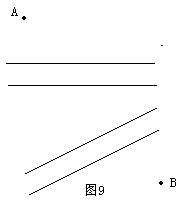
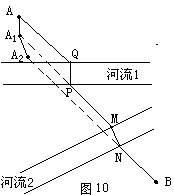
方法1:如图10,先将点A沿与河流1河岸垂直的方向平移一个河宽到A1,再沿与河流2河岸垂直的方向平移一河宽到A2,连接A2B,交河流2河岸于N,此处建桥MN;连接A1M,交河流1于P,在此处建桥PQ。所得路径AQPMNB最短。
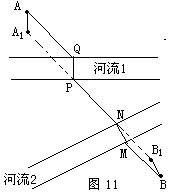
方法2:也可以将A沿与河流1垂直的方向平移1个河宽,得到A1,再将B沿与河流2河岸垂直的方向平移1个河宽得到B1,连接A1B1与河流1、河流2分别相交于N、P,分别作桥MN、PQ。所得路径AQPNMB最短。
由以上拓展,我们不难体会到,造桥选址问题,要使所得到的路径最短,就是要通过平移变换,使除桥长不变外所得到的其他路径经平移后在一条直线上。
作者简介:宋毓彬,男,1966年4月出生。中学数学高级教师。先后在《中学数学教学参考》、《中学生数学》、《数理天地》、《语数外学习》、〈数理化学习〉、〈数理化解题研究〉、〈中学课程辅导〉、〈数理报〉、〈学习报〉、〈数学周报〉、〈数学辅导报〉、〈小博士报〉、〈数字世界报〉发表初中数学辅导类文章80多篇。致力于初中数学教学与中考方面的研究。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |