2012中考数学考点 倍角三角形

倍角三角形中的一个结论

湖北省黄石市下陆中学　宋毓彬

例1（天津市中考题）在△ABC中，∠A、∠B、∠C所对应的边分别用a、b、c表示。

⑴如图1，在△ABC中，∠A=2∠B，且∠A=60°。求证：a²=b（b+c）

⑵如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”。本题第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角△ABC，如图2，∠A=2∠B，关系式a²=b（b+c）是否仍然成立？并证明你的结论。

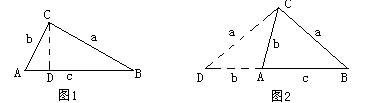
分析：⑴在△ABC中，∠A=2∠B，且∠A=60°，△ABC为Rt△，∠C=90°。

证法1：Rt△ACB中a=c，b=c，

所以a²=（c）²=

所以a²=b（b+c）。

⑵对于任意的倍角△ABC，∠A=2∠B，关系式a²=b（b+c）仍然成立。

如图2，延长BA至D，使AD=AC=b，连CD。

则∠CAB=2∠D，∴∠B=∠D，BC=CD=a，

由△ADC∽△CDB   ，即。

所以a²=b（b+c）。

由以上的证明，可以得到关于倍角三角形的一个结论：一个三角形中有一个角等于另一个角的两倍，2倍角所对边的平方等于一倍角所对边乘该边与第三边的和。

（例2中另外两种证法同样可证得a

例2(2009年全国初中数学联赛)在△ABC中，最大角∠A是最小角∠C的2倍，且AB=7，AC=8。则BC=（   ）

（A）7   （B）10   （C）    （D）7

分析：此题由例1中的结论，则BC²=7（7+8）=105，所以BC=

以下还可以提供几种解法供参考。

解法一：分割法。

如图1，作∠CAB的平分线AD交BC于D。

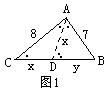
△ABC∽△DBA， ==，

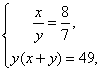∴解得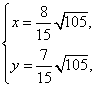∴ x+y=。

评析：解法一的思路是常规思路，平分倍角构造相似三角形，通过相似比得到方程组求出线段长，进而求出BC的长。但这种方法中，二元二次方程组的计算较为复杂。

解法二：构造法。

如图2，延长CA至点D，使AD=AB。

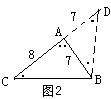
则∠D=∠ABD=∠CAB=∠C，

△CBD∽△DAB，=，

∴BD²=AB·CD=7×（8+7）=105，BD=，

又∠C=∠D，∴BC=BD=。

评析：利用二倍角为外角构造等腰三角形也是常见的作辅助线的技巧。BD为相似三角形比例中项，与方法一相比，计算相对简单。

解法三：综合法

作∠CAB的平分线AD交BC于D。作BE∥AD。

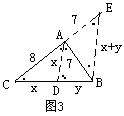
△ADC∽△BAE，=，①

△ADC∽△EBC，=，②

①×②，=，（x+y）²=7×15，x+y=

解析：由△ADC∽△BAE，BE∥AD，方法三事实上已将方法一、方法二统一了起来。所反映的本质是相同的。