巧构图形应用勾股定理
湖北省黄石市下陆中学 宋毓彬 湖北省黄石市二十一中 皮学军
构造图形，运用几何图形的直观性和数形结合的思想方法，应用勾股定理可以解决一些十分棘手的代数问题。
一、证明不等式
例1 试比较
－
与
（x＞y＞0）的大小，并说明你的理由。 解：因为（）2=（）2+（）2，联想到勾股定理，以、
为边作如图1所示的直角三角形，则其斜边长为
。由三角形两边之差小于第三边，－＜。 
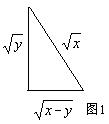
例2 已知a、b、c均为非负数，求证：
+
+
≥
（a+b+c） 分析：由题设条件联想到正方形对角线及勾股定理。
证明：如图2，以（a+b+c）为边长作正方形，并在两个邻边上按a、b、c大小将正方形分割成不同的矩形。
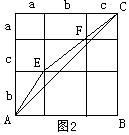
由勾股定理可求得：
AE=，EF=，FC=
AC=（a+b+c）
因为AE+EF+FC≥AC
所以+
+≥（a+b+c）。
二、求特殊三角形面积
例3 若a、b均为正数，且、
、
是一个三角形的三边长。那么这个三角形的面积等于 。 分析：直接用三角形面积公式求面积较为复杂，构造图形求面积则更简便。
解：如图3，分别以2 a、2b为边长作矩形ABCD。取AB、BC中点E、F，连接EF、DF、DE。
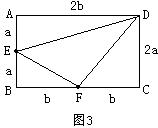
由勾股定理，可求得：
EF=，FD=
，ED= 故△EFD即为题设三角形。
S△EFD=S矩形ABCD－S△AED－S△BEF－S△CFD
=4ab－ab－
ab－ab=
ab。
三、求线段和的最小值
例4 已知正数a、b满足a+b=2。求u=
+
的最小值。
分析：由a+b=2，u=
+
= u=+
，构造合适图形可将其转化为求两条线段和的最小值问题。 解：由a+b=2，u=+
=+
构造如图4的图形，取AC=2，BD=1，CD=2，作A关于CD的对称点A′，连接A′B交CD于P，设PC=a，则PD=2－a，AP=
，BP=。此时A′B=AP+BP为最小值。 
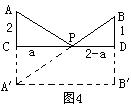
又作A′B′⊥BD于B′，则A′B′=CD=2，BB′=2+1=3
Rt△A′BB′中，A′B=
=
。即u的最小值为13。
练习题：
1.对于正数a、b、c、d，如果a+b=c+d，试比较
+
与（a+b）的大小。（提示：a+b=c+d为边构造正方形，再分割成a、b、c、d为边的矩形，用勾股定理证明）
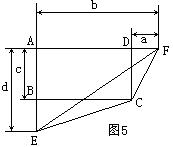
2.设a、b、c、d为正实数，a＜b，c＜d，bc＞ad，有一个三角形的三边长分别为、
、
，求此三角形的面积。 （提示：构造如图5的图形求解）
3.求代数式
+
的最小值。
（提示：将原式变形为+
，仿例4，取CD=12。）
作者简介：宋毓彬，男，44岁，中学数学高级教师。在《中学数学教学参考》、《数理天地》、《中学生数学》、《语数外学习》、《数理化学习》、《数理化解题研究》、《中学课程辅导》、《数学周报》、《数学辅导报》《数理报》、《小博士报》等报刊发表教学辅导类文章70多篇。主要致力于初中数学中考及解题方法、技巧等教学方面的研究。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |