双曲线中的面积问题
湖北省黄石市下陆中学 宋毓彬
学习反比例函数时，我们经常遇到一些求解与其函数图象双曲线有关的面积问题。要解决好这些问题，应注意以下几个方面的基础知识：
设反比例函数式为y=
。
⑴由双曲线上一点向两条坐标轴做垂线段，由这两条垂线段与两坐标州围成的矩形的面积计算。（如图1，以第一象限的图象为例）
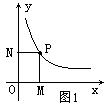
由四边形PMON为矩形。设P点坐标为（m，n），P在y=图象上，则有mn=k。∵OM=
，ON=
∴S四边形OMPN=OM·ON=·
=
=
⑵由双曲线上一点向其中一条坐标轴的作垂线段，并连接这一点与原点的线段，由这两条线段与坐标轴围成的三角形的面积的计算。（如图2，仍以第一象限的图象为例）
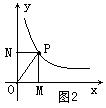
由图象可知，S△
POM=S△PON=
S四边形OMPN=。 ⑶理解点的坐标的几何意义：点P的坐标为（m，n），则表示P到y轴的距离；表示P到x轴的距离。
⑷用好双曲线的对称性：双曲线关于原点O对称，因此双曲线y=
与过原点O的正比例函数y=k2x的交点关于原点O对称。 ⑸会利用反比例函数关系式y=设双曲线上点的坐标。如点P在双曲线y=的图象上，设P点的横坐标为m，则P点的坐标可表示为（m，
）
⑹会用割补法求面积。尤其要注意有时需先利用坐标轴构造出特殊图形（如矩形、梯形、直角三角形等）。
一、用好双曲线的对称性
例1 若函数y=kx（k＞0）与函数y=
的图象相交于A、C两点，AB⊥x轴于B。则△ABC的面积为（ ）。
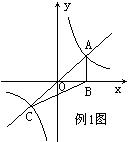
A。1 B。2 C。3 D。4
解：由A在双曲线y=上，AB⊥x轴于B。
∴S
△ABO=×1= 又由A、B关于O对称，S△CBO= S△ABO=
∴S△ABC= S△CBO+S△ABO=1 故选（A）
二、正确理解点的坐标的几何意义
例2 如图，反比例函数y=－
与一次函数y=－x+2的图象交于A、B两点，交x轴于点M，交y轴于点N，则S△AOB= 。
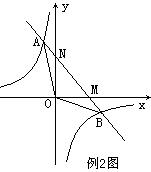
解：由y=－x+2交x轴于点M，交y轴于点N
M点坐标为（2，0），N点坐标为（0，2） ∴OM=2，ON=2
由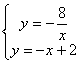
解得
或
∴A点坐标为（－2，4），B点坐标为（4，－2）
S△AOB=S△AON+S△MON+S△BOM
=ON·
+OM·ON+OM·
=6 （或S△AOB=S△AOM+S△BOM=OM·
+
OM·=6）
三、注意分类讨论
例3 如图，正方形OABC的面积为9，点O是坐标原点，点A在x轴上，点C在y轴上，点B在函数y=（k＞0，x＞0）的图象上。点P（m、n）是函数函数y=上任意一点，过点P分别作x轴、y轴的垂线。垂足分别为E、F，并设矩形OEPF中和正方形OABC不重合部分的面积为S。
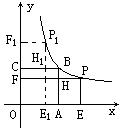
⑴求点B的坐标和k值。
⑵当S=
时，求P点的坐标。
解：⑴设B点坐标为（x0，y0），B在函数y=（k＞0，x＞0）的图象上，∴S正方形OABC= x0y0=9，∴x0=y0=3
即点B坐标为（3，3），k= x
0y0=9⑵①当P在B点的下方（m＞3）时。
设AB与PF交于点H，∵点P（m、n）是函数函数y=
上，
∴S四边形CEPF=mn=9，S矩形OAHF=3n
∴S=9－3n=，解得n=
。当n=时，
=，即m=6 ∴P点的坐标为（6，）
②当P在B点的上方（m＜3）时。 同理可解得：P1点的坐标为（，6）
∴当S=时，P点的坐标为（6，
）或（，6）。
四、善用“割补法”
例4 如图，在直角坐标系xOy中，一次函数y=k1x+b的图象与反比例函数y=
的图象相交于A（1，4），B（3，m）两点。
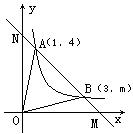
⑴求一次函数解析式；⑵求△AOB的面积。
解：⑴由A（1，4），在y=的图象上，∴k2=xy=4
B（3，m）在y=
的图象上，∴B点坐标为（3，
）
A（1，4）、B（3，）在一次函数y=k1x+b的图象上，
可求得一次函数解析式为：y=－
x+
。 ⑵设一次函数y=－x+交x轴于M，交y轴于N（如图）。则M（4，0），N（0，）
S△AOB=S△MON－S△OBM－S△AON=OM·ON—
OM－ON =×4×－
×4×－××1=
五、构造特殊辅助图形
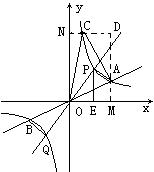
例5 如图，已知直线y=
x与双曲线y=（k＞0）交于A、B两点，且点A横坐标为4。⑴求k的值；⑵若双曲线y=（k＞0）上一点C的纵坐标为8，求△AOC的面积。⑶过原点O的另一条直线交双曲线y=（k＞0）于P、Q两点（P点在第一象限），若由点ABPQ为顶点组成的四边形面积为24，求点P的坐标。
解：⑴A横坐标为4，在直线y=x上，A点坐标为（4，2）
A（4，2）又在y=上，∴k=4×2=8
⑵C的纵坐标为8，在双曲线y=上，C点坐标为（1，8）
过A、C分别作x轴、y轴垂线，垂足为M、N，且相交于D，则得矩形ONDM。S
矩形ONDM=4×8=32。又S△ONC=4，S△CDA=9，S△OAM=4
∴S△AOC= S矩形ONDM―S△ONC―S△CDA―S△OAM=32―4―9―4=15
⑶由反比例函数图象是中心对称图形，OP=OQ，OA=OB，
∴四边形APBQ是平行四边形。S△POA=
S四边形APBQ=6
设P点的坐标为（m，
），过P、A分别作x轴、y轴垂线，垂足为E、M。 ∴S△POE=S△AOM=k=4
①若0＜m＜4时，如图所示。
∵S△PEO+S梯形PEMA=S△POA+S△AOM，∴S梯形PEMA=S△POA=6
∴（2+）（4－m）=6 解得m=2或m=－8（舍去） P点的坐标为（2，4）
②若m＞4时，同理可求得m=8或m=－2（舍去），P点的坐标为（8，1）
作者简介：宋毓彬，男，45岁，中学数学高级教师。在《中学数学教学参考》、《数理天地》、《中学生数学》、《数理化学习》、《数理化解题研究》、《中学课程辅导》、《数学周报》、《数学辅导报》、《数理报》、《小博士报》、《少年智力开发报》等报刊发表教学辅导类文章60多篇。主要致力于初中数学中考及解题方法、技巧等教学方面的研究。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |