2013中考数学备考：直线与圆

证明直线与圆相切主要有以下两种方法：

一、根据切线的判定定理

经过半径的外端并且垂直于这条半径的直线是圆的切线。

当已知直线与圆有公共点时，常用此法。辅助线是连结公共点和圆心，只要设法证明直线与半径垂直即可。

例1. （2004年江苏省淮安市中考题）

已知：如图1，在△ABC中，∠BAC的平分线AD交△ABC的外接圆⊙O于点D，交BC于点G。

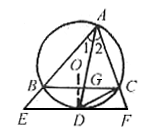
图

（1）连结CD，若AG＝4，DG＝2，求CD的长；（解略）

（2）过点D作EF∥BC，分别交AB、AC的延长线于点E、F。求证：EF与⊙O相切。

证明：（2）连结OD，由∠1＝∠2，

得，则OD⊥BC

所以

因为EF∥BC，所以∠BCD＝∠CDF

从而

即EF⊥OD，所以EF与⊙O相切。

例2. （2002年湖北省黄冈市中考题）

如图2，BE是⊙O的直径，点A在BE的延长线上，弦PD⊥BE，垂足为C，连结OD，且∠AOD＝∠APC。

（1）求证：AP是⊙O的切线。

（2）略。

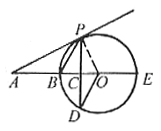
图2

证明：连结OP，因为PD⊥BE，OP＝OD

所以∠POB＝∠DOB，而∠APD＝∠DOB

所以∠POB＝∠APD

由PD⊥BE得：∠POB＋∠OPC＝90°

即∠APD＋∠OPC＝90°

所以AP是⊙O的切线

二、根据直线与圆的位置关系

若圆心到直线的距离等于圆的半径，则直线与圆相切。

当题设中不能肯定直线与圆有公共点时，常用此法。辅助线是过圆心作该直线的垂线段，只要设法证明垂线段等于半径即可。

例3. （2003年甘肃省中考题）

如图3，Rt△ABC中，∠C＝90°，AC＝3cm，BC＝4cm，以C为圆心、r为半径作圆，当r＝2.4时，AB与圆有怎样的位置关系？为什么？

图3

解：作CD⊥AB，垂足为D，则

由CD·AB＝AC·BC得：

即AB与圆相切。

例4. 如图4，AB是⊙O的直径，AC⊥l，BD⊥l，C、D为垂足，且AC＋BD＝AB，求证：直线l与⊙O相切。

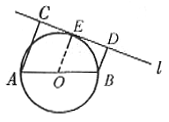
图4

证明：过O作OE⊥l，E为垂足，则

OE∥AC∥BD，又AO＝BO

所以

而，则

即垂线段OE等于圆的半径，所以直线l是⊙O的切线。