行测数量关系答题技巧你掌握了多少?出国留学网小编为大家提供行测数学运算不定方程的三种常用解法,一起来看看吧!祝大家备考顺利!
行测数学运算不定方程的三种常用解法
在行测运算题当中,设方程是常用的技巧,含有未知数的等式叫做方程。不定方程中未知数的个数多于独立方程的个数。比如:x+y=5。在行测里也经常列出不定方程,但是很多人都不会解。其实只要掌握好三种常用的方法,问题自然迎刃而解。
1、整除法:利用不定方程中各数能被同一个数整除的关系来求解。
例1:小张的孩子出生的月份乘以29,出生的日期乘以24,所得的两个乘积加起来刚好等于900。问孩子出生在哪一个季度?
A.第一季度 B.第二季度 C.第三季度 D.第四季度
【答案】D
【解析】关键词:等于,所以找到等量关系。设出生月份为x,出生的日期为y。29x+24y=900,24与900的最大公约数为12,意味着24y能被12整除,900能被12整除,29为质数,所以x能被12整除,由于12表示的是月份,所以是第四季度。
2、奇偶性:未知数的系数奇偶性不同
例2:办公室工作人员使用红、蓝两种颜色的文件袋装29份相同的文件。每个红色文件袋可以装7份文件,每个蓝色文件袋可以装4份文件。要使每个文件袋都恰好装满,需要红色、蓝色文件袋的数量分别为()个。
A.1、6 B.2、4 C.4、1 D.3、2
【答案】D
【解析】由题可知袋子的个数肯定是为整数,设红色袋子数量为x,蓝色袋子数量为y,由题意可得7x+4y=29,此时未知数的系数为7和4,奇偶性不同。4y为偶数,29为奇数,则 7x为奇数,得出x为奇数,排除B、C。接下来代入A选项,x=1,y不是整数,排除A,选择D。验证:x=3,y=2满足题意。
3、尾数法:未知数的系数是5的倍数
超市将99个苹果装进两种包装盒,大包装盒每个装12个苹果,小包装盒每个装5个苹果,共用了十多个盒子刚好装完。问两种包装盒相差多少个?
A.3 B.4 C.7 D.13
【答案】D
【解析】由题可知,大包装盒的个数和小包装盒的个数为整数,设大包装盒的个数为x,小包装盒为y,可得到12x+5y=99,x+y>10。5y尾数只能是0、5,对应的12x的尾数只能是9、4,又因为12x为偶数,所以尾数只能是4。当x=2时,y=15,x+y=17,满足题意。15-2=13;当x=7,y=3,x+y=10,不满足题意,选择D。
行测数学运算答题技巧:就是对“你”有感觉
很多考生备考行测很长一段时间之后对数量关系还是把握不好技巧,今天教育专家就给大家总结一下,有些题型自带特点,让人没有办法对它没感觉。带领大家感受一下,如果大家在备考中遇到了,就不用绕道而行了。
1、和定最值问题题干特征:题目中出现最大、最小、极大、极小的字眼。
解题思路:问最大,其他项满足尽量小;问最小,其他项满足尽量大。
例题展示; 5名学生参加某科学竞赛,共得91分,已知每个人的得分各不相同,最高得21分,则最低分最低是多少( )。
A.13 B.14 C.15 D.16
【解析】求最小值最小,原则是其他的尽可能大,各得21、20、19、18分,91-(21+20+19+18)=13,选A。
2、最不利问题题干特征:至少…才能保证
解题思路:最倒霉的情况+1
例题展示:某企业要从9名候选人中投票选举企业的中层管理者。假定每个员工必须投票且只能投票选举三位候选人,若要保证至少两个的员工所投的票是相同的三名候选人,那么企业员工数至少有多少人?
A.84 B.85 C.86 D.87

行测数量关系行程问题模拟题及答案
1、小陈骑车自A地往B地,先上坡后下坡,到达B地后立即返回A地,共用19分钟。已知小陈的上坡速度为350米/分钟,下坡速度为600米/分钟,则A地距离B地( )米。
A.3600 B.4200 C.4600 D.5400
【解析】小陈从A到B,然后又从B返回A,这说明在这样一个过程中,他们所走的路程是相等的,那么根据正反比,速度之比是7:12,所以得出时间之比就是12:7,这样我们就能知道上坡的时间是12分钟,S=VT,所以S=350×12=4200,答案选B。
2、两辆汽车同时从两地相向开出,甲车每小时行驶60千米,乙车每小时行驶48千米,两车在离两地中点48千米处相遇,则两地相距( )千米。
A.192 B.224 C.416 D.864
【解析】从题干中我们发现两者的速度之比是5:4,因为他们所走的时间是相同的,所以,路程之比同样是5:4,这样,甲比乙多走一份,所以中间部分是距离端点4.5份,即0.5份对应的路程是48千米,所以S=48×18=864,答案选D。
3、甲乙两车同时从A、B两地相向而行,在距B地54千米处相遇,它们各自到达对方车站后立即返回,在距A地42千米处相遇。请问A、B两地相距多少千米?
A.120 B.100 C.90 D.80
【解析】甲从A出发,乙从B出发,第一次相遇,在距离B点54千米处,说明乙走了54千米,而第二次相遇。距离A点42千米,说明乙到达A点后返回时,距离A点42千米,所以对于乙而言总共走了54×3=162,全程等162-42=120,答案A。
4、一片草场上草每天都均匀地生长,如果放24头牛,则6天吃完牧草;如果放21头牛,则8天吃完牧草。问如果放16头牛,几天可以吃完牧草?
A.12 B.14 C.16 D.18
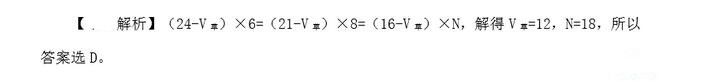
5、 甲、乙两地铁路线长1880千米,从甲地到乙地开出一辆动车,每小时行驶160千米,3小时后,从乙地到甲地开出一辆高铁,经4小时后与动车相遇,则高铁每小时行驶:
A.180千米 B.190千米
C.200千米 D.210千米
【解析】动车3小时行驶了160×3=480千米,则4小时高铁和动车共行驶了1880-480=1400千米,每小时共行驶1400÷4=350千米,高铁每小时行驶350-160=190千米,选择B。
6、甲、乙两人沿直线从A地步行至B地,丙从B地步行至A地。已知甲、乙、丙三人同时出发,甲和丙相遇后5分钟,乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问A、B两地距离为多少米?
A.8000米 B.8500米 C.10000米 D.10500米
【答案】D。解析:甲、丙相遇时,甲比乙多走了的距离为乙、丙相距的(75+65)×5=700米,所以此时三人都已步行了700÷(85-75)=70分钟,故A、B两地距离为(85+65)×70=10500米。
7、甲乙两人早上10点同时出发匀速向对方的工作单位行进,10点30分两人相遇并继续以原速度前行。10点54分甲到达乙的工作单位后,立刻原速返回自己单位。问甲返回自己单位时,乙已经到了甲的工作单位多长时间了?( )
A.42分 B.40分30秒
C.43分30秒 D.45分
【答案】B。解析:由题意知,乙30分钟的路程,甲需要10点54分-10点30分=24分走完,故甲、乙相同路程所需的时间比为24∶30=4∶5,可得乙从相遇到甲的工作单位需要30×5÷4=37.5分。甲从相遇到返回自己单位共用时24+24+30=78分,所求为78-37.5=40.5分=40分30秒,选B。
小编精心为您推荐:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |