分式运算的技巧
【精练】计算:![]()
【分析】本题中有四个分式相加减,如果采用直接通分化成同分母的分式相加减,公分母比较复杂,其运算难度较大.不过我们注意到若把前两个分式相加,其结果却是非常简单的.因此我们可以采用逐项相加的办法.
【解】![]() =
=
=![]()
=![]()
【知识大串联】
1.分式的有关概念
设A、B表示两个整式.如果B中含有字母,式子![]() 就叫做分式.注意分母B的值不能为零,否则分式没有意义
就叫做分式.注意分母B的值不能为零,否则分式没有意义
分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简
2、分式的基本性质
![]()
![]() (M为不等于零的整式)
(M为不等于零的整式)
3.分式的运算
(分式的运算法则与分数的运算法则类似).

4.零指数 ![]()
5.负整数指数 ![]()
注意正整数幂的运算性质 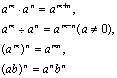
可以推广到整数指数幂,也就是上述等式中的m、 n可以是O或负整数.
分式是初中代数的重点内容之一,其运算综合性强,技巧性大,如果方法选取不当,不仅使解题过程复杂化,而且出错率高.下面通过例子来说明分式运算中的种种策略,供同学们学习参考.
1.顺次相加法
例1:计算:![]()
【分析】本题的解法与例1完全一样.
【解】![]() =
=![]()
=
=![]()
2.整体通分法
【例2】计算:![]()
【分析】本题是一个分式与整式的加减运算.如能把(-a-1)看作一个整体,并提取“-”后在通分会使运算更加简便.通常我们把整式看作分母是1的分式.
【解】
3.化简后通分
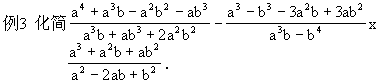
分析:直接通分,极其繁琐,不过,各个分式并非最简分式,有化简的余地,显然,化简后再通分计算会方便许多.
![]()
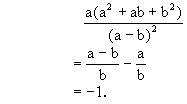
4.巧用拆项法
例4计算:![]() .
.
分析:本题的10个分式相加,无法通分,而式子的特点是:每个分式的分母都是两个连续整数的积(若a是整数),联想到![]() ,这样可抵消一些项.
,这样可抵消一些项.
解:原式=![]()
=![]()
=![]() =
=![]()
5.分组运算法
例5:计算:
分析:本题项数较多,分母不相同.因此,在进行加减时,可考虑分组.分组的原则是使各组运算后的结果能出现分子为常数、相同或倍数关系,这样才能使运算简便.
解:![]()
=![]()
=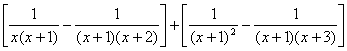
=
=![]()
=![]()
【错题警示】
一、错用分式的基本性质
例1 化简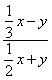
错解:原式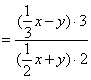
![]()
分析:分式的基本性质是“分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变”,而此题分子乘以3,分母乘以2,违反了分式的基本性质.
正解:原式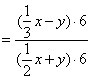
![]()
二、错在颠倒运算顺序
例2 计算![]()
错解:原式![]()
分析:乘除是同一级运算,除在前应先做除,上述错解颠倒了运算顺序,致使结果出现错误.
正解:原式![]()
三、错在约分
例1 当![]() 为何值时,分式
为何值时,分式![]() 有意义?
有意义?
[错解]原式![]() .
.
由![]() 得
得![]() .
.
∴![]() 时,分式
时,分式![]() 有意义.
有意义.
[解析]上述解法错在约分这一步,由于约去了分子、分母的公因式![]() ,扩大了未知数的取值范围,而导致错误.
,扩大了未知数的取值范围,而导致错误.
[正解]由![]() 得
得![]() 且
且
∴当![]() 且
且![]() ,分式
,分式![]() 有意义.
有意义.
四、错在以偏概全
例2 ![]() 为何值时,分式
为何值时,分式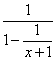 有意义?
有意义?
[错解]当![]() ,得
,得![]() .
.
∴当![]() ,原分式有意义.
,原分式有意义.
[解析]上述解法中只考虑![]() 的分母,没有注意整个分母
的分母,没有注意整个分母![]() ,犯了以偏概全的错误.
,犯了以偏概全的错误.
[正解]
由![]() ,得
,得![]() .
.
∴当![]() 且
且![]() 时,原分式有意义.
时,原分式有意义.
五、错在计算去分母
例3 计算![]() .
.
[错解]原式![]()
=![]() .
.
[解析]上述解法把分式通分与解方程混淆了,分式计算是等值代换,不能去分母,.
[正解]原式![]()
![]() .
.
六、错在只考虑分子没有顾及分母
例4 当![]() 为何值时,分式
为何值时,分式![]() 的值为零.
的值为零.
[错解]由![]() ,得
,得![]() .
.
∴当
[解析]当![]() 时,分式的分母
时,分式的分母![]() ,分式无意义,谈不上有值存在,出错的原因是忽视了分母不能为零的条件.
,分式无意义,谈不上有值存在,出错的原因是忽视了分母不能为零的条件.
[正解]由由![]() ,得
,得![]() .
.
由![]() ,得
,得![]() 且
且![]() .
.
∴当![]() 时,原分式的值为零.
时,原分式的值为零.
七、错在“且”与“或”的用法
例7 ![]() 为何值时,分式
为何值时,分式
错解:要使分式有意义,![]() 须满足
须满足![]() ,即
,即![]() .
.
由![]() 得
得![]() ,或由
,或由![]() 得
得
![]() 当
当![]() 或
或![]() 时原分式有意义.
时原分式有意义.
分析:上述解法由![]() 得
得![]() 或
或
故本题的正确答案是![]() 且
且![]() .
.
八、错在忽视特殊情况
例8 解关于![]() 的方程
的方程![]() .
.
错解:方程两边同时乘以![]() ,得
,得
当![]() 时,
时,![]() ,
,
当![]() 时,原方程无解.
时,原方程无解.
分析:当![]() 时,原方程变为
时,原方程变为
正解:方程两边同时乘以![]() ,得
,得![]() ,即
,即![]()
当![]() 且
且![]() 时,
时,![]() ,当
,当![]() 或
或![]() 时,原方程无解.
时,原方程无解.
【分析】本题中有四个分式相加减,如果采用直接通分化成同分母的分式相加减,公分母比较复杂,其运算难度较大.不过我们注意到若把前两个分式相加,其结果却是非常简单的.因此我们可以采用逐项相加的办法.
【解】![]() =
=
=![]()
=
【知识大串联】
1.分式的有关概念
设A、B表示两个整式.如果B中含有字母,式子![]() 就叫做分式.注意分母B的值不能为零,否则分式没有意义
就叫做分式.注意分母B的值不能为零,否则分式没有意义
分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简
2、分式的基本性质
![]()
![]() (M为不等于零的整式)
(M为不等于零的整式)
3.分式的运算
(分式的运算法则与分数的运算法则类似).
![]() (异分母相加,先通分);
(异分母相加,先通分);

4.零指数 ![]()
5.负整数指数
注意正整数幂的运算性质 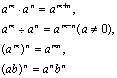
可以推广到整数指数幂,也就是上述等式中的m、 n可以是O或负整数.
分式是初中代数的重点内容之一,其运算综合性强,技巧性大,如果方法选取不当,不仅使解题过程复杂化,而且出错率高.下面通过例子来说明分式运算中的种种策略,供同学们学习参考.
1.顺次相加法
例1:计算:![]()
【分析】本题的解法与例1完全一样.
【解】![]() =
=![]()
=![]()
=![]()
2.整体通分法
【例2】计算:![]()
【分析】本题是一个分式与整式的加减运算.如能把(-a-1)看作一个整体,并提取“-”后在通分会使运算更加简便.通常我们把整式看作分母是1的分式.
【解】![]() =
=
3.化简后通分
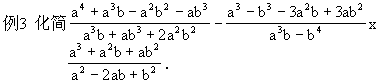
分析:直接通分,极其繁琐,不过,各个分式并非最简分式,有化简的余地,显然,化简后再通分计算会方便许多.
![]()
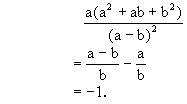
4.巧用拆项法
例4计算:![]() .
.
分析:本题的10个分式相加,无法通分,而式子的特点是:每个分式的分母都是两个连续整数的积(若a是整数),联想到![]() ,这样可抵消一些项.
,这样可抵消一些项.
解:原式
= =![]()
=![]() =
=
5.分组运算法
例5:计算:![]()
分析:本题项数较多,分母不相同.因此,在进行加减时,可考虑分组.分组的原则是使各组运算后的结果能出现分子为常数、相同或倍数关系,这样才能使运算简便.
解:![]()
=![]()
=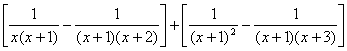
=![]()
=![]()
=![]()
【错题警示】
一、错用分式的基本性质
例1 化简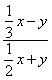
错解:原式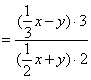
分析:分式的基本性质是“分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变”,而此题分子乘以3,分母乘以2,违反了分式的基本性质.
正解:原式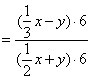
二、错在颠倒运算顺序
例2 计算![]()
错解:原式
分析:乘除是同一级运算,除在前应先做除,上述错解颠倒了运算顺序,致使结果出现错误.
正解:原式![]()
例1 当![]() 为何值时,分式
为何值时,分式![]() 有意义?
有意义?
[错解]原式![]() .
.
由![]() 得
得![]() .
.
∴![]() 时,分式
时,分式
[解析]上述解法错在约分这一步,由于约去了分子、分母的公因式![]() ,扩大了未知数的取值范围,而导致错误.
,扩大了未知数的取值范围,而导致错误.
[正解]由![]() 得
得
∴当![]() 且
且
四、错在以偏概全
例2 ![]() 为何值时,分式
为何值时,分式
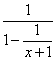 有意义?
有意义? [错解]当![]() ,得
,得![]() .
.
∴当![]() ,原分式有意义.
,原分式有意义.
[解析]上述解法中只考虑![]() 的分母,没有注意整个分母
的分母,没有注意整个分母![]() ,犯了以偏概全的错误.
,犯了以偏概全的错误.
[正解] ![]() ,得
,得![]() ,
,
由![]() ,得
,得
∴当![]() 且
且![]() 时,原分式有意义.
时,原分式有意义.
五、错在计算去分母
例3 计算![]() .
.
[错解]原式![]()
=![]() .
.
[解析]上述解法把分式通分与解方程混淆了,分式计算是等值代换,不能去分母,.
[正解]原式![]()
![]() .
.
六、错在只考虑分子没有顾及分母
例4 当![]() 为何值时,分式
为何值时,分式![]() 的值为零.
的值为零.
[错解]由![]() ,得
,得
∴当![]() 或
或![]() 时,原分式的值为零.
时,原分式的值为零.
[解析]当![]() 时,分式的分母
时,分式的分母![]() ,分式无意义,谈不上有值存在,出错的原因是忽视了分母不能为零的条件.
,分式无意义,谈不上有值存在,出错的原因是忽视了分母不能为零的条件.
[正解]由由![]() ,得
,得
由![]() ,得
,得![]() 且
且
∴当![]() 时,原分式的值为零.
时,原分式的值为零.
七、错在“且”与“或”的用法
例7 ![]() 为何值时,分式
为何值时,分式
错解:要使分式有意义,![]() 须满足
须满足![]() ,即
,即
由![]() 得
得![]() ,或由
,或由
![]() 当
当
分析:上述解法由![]() 得
得
故本题的正确答案是![]() 且
且
八、错在忽视特殊情况
例8 解关于![]() 的方程
的方程
错解:方程两边同时乘以![]() ,得
,得![]() ,即
,即
当![]() 时,
时,![]() ,
,
当![]() 时,原方程无解.
时,原方程无解.
分析:当![]() 时,原方程变为
时,原方程变为![]() 取任何值都不能满足这个方程,错解只注意了对
取任何值都不能满足这个方程,错解只注意了对
正解:方程两边同时乘以![]() ,得
,得
当![]() 且
且![]() 时,
时,
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |