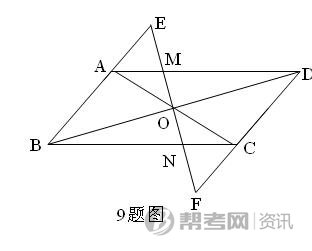
1.(2011重庆市,9,4分)如图,在平行四边形ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①AO=BO;②OE=OF;③△EAM∽△EBN;④△EAO≌△CNO,其中正确的是
A.①② B.②③ C.②④ D.③④
考点:相似三角形的判定与性质;全等三角形的判定与性质;平行四边形的性质。
分析:①根据平行四边形的对边相等的性质即可求得AO≠BO,即可求得①错误;②易证△AOE≌△COF,即可求得EO=FO;③根据相似三角形的判定即可求得△EAM∽△EBN;④易证△EAO≌△FCO,而△FCO和△CNO不全等,根据全等三角形的传递性即可判定该选项错误。
答案:解:①平行四边形中邻边垂直则该平行四边形为矩形,故本题中AC≠BD,即AO≠BO,故①错误;②∵AB∥CD,∴∠E=∠F,又∵∠EOA=∠FOC,AO=CO∴△AOE≌△COF,∴OE=OF,故②正确;③∵AD∥BC,∴△EAM∽△EBN,故③正确;④∵△AOE≌△COF,且△FCO和△CNO,故△EAO和△CNO不相似,故④错误,即②③正确。故选B.
点评:本题考查了相似三角形的判定,考查了全等三角形对应边相等的性质,考查了平行四边形对边平行的性质,本题中求证△AOE≌△COF是解题的关键。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |