2012中考数学考点 平方差公式

妙用平方差公式巧解题

甘肃省镇原县王寨初中　慕志明

用平方差公式能迅速准确地算出复杂难算题的答案，现用下列例题揭示利用平方差公式解答计算题的方法和技巧，希望对大家能有所启发和帮助。

例1　已知：a+3b=-2,求a+2a-6b-9b的值。

解：a+2a-6b-9b＝a-9b+2a-6b＝（a-9b）+（2a-6b）＝（a+3b)(a-3b)+2(a-3b)=(a-3b)(a+3b+2)=(a-3b)(-2+2)=0。

如果在解题前不认真分析，不对算式进行科学组合，就很难找到用平方差公式和提取公因式解题的突破口，可见：解题前的观察分析对解题非常重要。

例2　计算。

解：分子＝2001－22001－1999＝2001－22001－2001+2＝2001（2001－2）－（2001－2）＝（2001－2）（2001－1），

分母＝2001+2001－2002＝2001+2001－2001－1＝2001（2001+1）－（2001+1）＝（2001+1）（2001－1）。

所以就有：＝＝＝。

如果在解题前不对算式进行认真仔细地观察，就很难发现“1999＝2001－2，2002＝2001+1”，就更难发现分子中的公因式是“2001－2”，分母中的公因式是“2001+1”，“2001”是分子和分母中共同的公因式，由于找到了分子和分母中的公因式，才利用提取公因式法和平方差公式顺利的得出了此题的准确答案。

例3　计算（2+1）（2+1）（2+1）（2+1）。

解法1：（2+1）（2+1）（2+1）（2+1）＝（2－1）（2+1）（2+1）（2+1）（2+1）（2－1）＝（2－1）（2+1）（2+1）（2+1）（2－1）＝（2－1）（2+1）（2+1）（2－1）＝（2－1）（2+1）（2－1）＝（2－1）（2－1）＝2－1＝65535，

因为：2＝22＝256256＝65536，2－1＝65536－1＝65535，

解法2：2＝22＝4，2＝22＝44＝16，2＝22＝1616＝256，

所以（2+1）（2+1）（2+1）（2+1）＝3517257＝65535。

解法1的解题者，由于在解题前认真观察分析清楚了算式中的数据规律，先给算式乘以（2－1），后给算式除以（2－1），虽然没有改变算式的值，但乘在算式前面的（2—1）和（2+1）却构成了平方差公式，这样由前向后逐个处理，就可顺利得到命题者所要的准确结果“2－1”，在算式最后除以“2－1”，实质是除以1，足见解法1中的解题者是多么的聪明。

解法2虽然一气呵成，直接算出了本题的准确答案。但却没有达到编者的意图，如果在计算过程中稍有不慎，就会得出错误的结果。其实本题命题者的本意是考查学生运用平方差公式解题的本领，只要解题者解出“2－1”就行，而并不是要求解题者能算出“65535”。因为该题面向的是八年级学生。

例4　计算100－99+98－97+96－95+…+6－5+4－3+2－1。

解：100－99＝（100+99）（100－99）＝199，

98－97＝（98+97）（98－97）＝195，

96－95＝（96+95）（96－95）＝191，

94－93＝（94+93）（94－93）＝187，

92－91＝（92+91）（92－91）＝183，

10－9＝（10+9）（10－9）＝19，

8－7＝（8+7）（8－7）＝15，

6－5＝（6+5）（6－5）＝11，

4－3＝（4+3）（4－3）＝7，

2－1＝（2+1）（2－1）＝3。

观察上述用平方差公式算得的结果可得，199－4＝195，195－4＝191，191－4＝187，15－4＝11，11－4＝7，7－4＝3.。这样就有：

100－99+98－97+96－95+…+6－5+4－3+2－1＝199+195+191+187+183+…+19+15+11+7+3。

观察“199+195+194+187+183+…+19+15+11+7+3”可发现：“199+3＝202，195+7＝202，191+11＝202，187+15＝202，183+19＝202”。只要能探究明白“199+195+194+187+183+…+19+15+11+7+3”中能加成多少个202，问题就会很快解决。只好用下述列表的方法探究“199+195+194+187+183+…+19+15+11+7+3”中究竟能加成多少个202：

由上表可以看出“199+195+194+187+183+…+19+15+11+7+3”中的数据，共能加出25个202，20225＝5050。

所以就有：

100－99+98－97+96－95+…+6－5+4－3+2－1

＝199+195+191+187+183+…+19+15+11+7+3

＝20225

＝5050。

您还有比上述算法更快捷准确的算法吗？请试试看！

一道难住初中物理教师的数学计算题

女儿向爸爸请教如下一道数学计算题，难住了给她教物理的爸爸，她的爸爸只好向数学专家请教，最终解决了问题，现共享于后，以求共同提高。

已知6x－9x+mx+n能被6x-x+4整除，求m和n的值。

解：这是一道初中学生还没有学的多项式相除问题，具体解法如下：

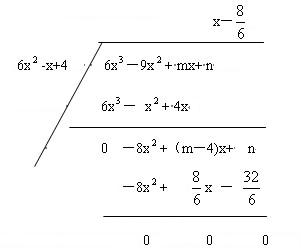
由上述计算结果可得：

（m－4)x－x=0，

m－4－＝0，

m－＝0，

m==，

n－（－）＝0，

n+＝0，

n=－=－，

您还有比这更妙的解法吗？请赐教！