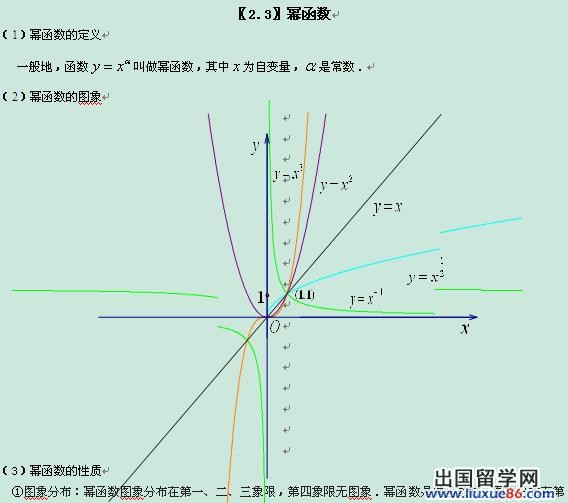
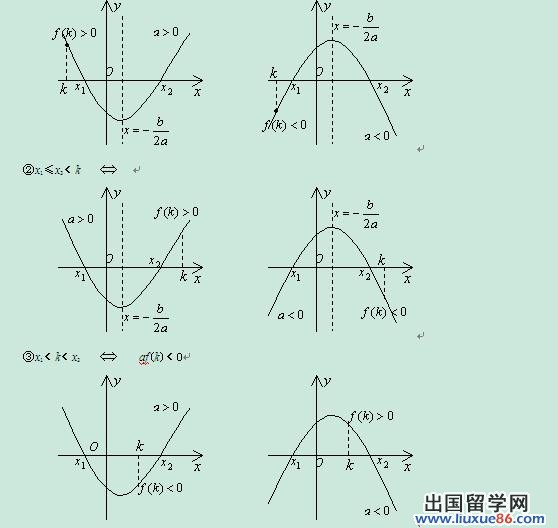
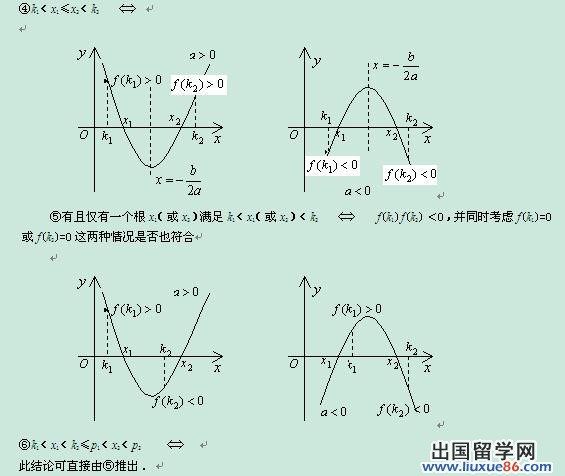
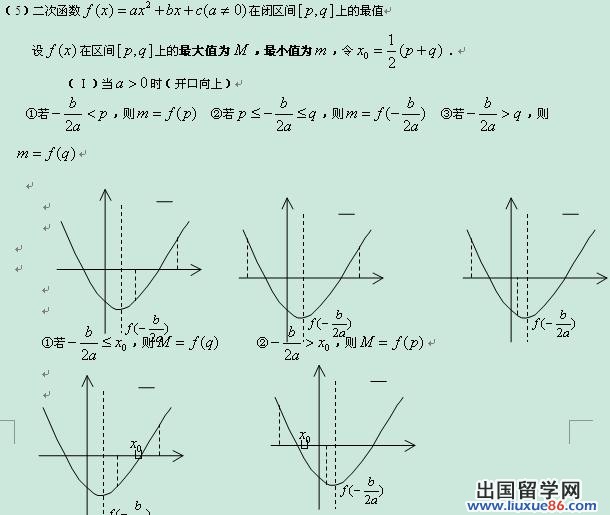
函数占据了初中数学知识点的很大部分,因此学好函数十分重要。下面是由出国留学网编辑为大家整理的“初中数学函数知识点归纳总结(实用)”,仅供参考,欢迎大家阅读本文。
一次函数知识点
1.一次函数
如果y=kx+b(k、b是常数,k≠0),那么y叫做x的一次函数。
特别地,当b=0时,一次函数y=kx+b成为y=kx(k是常数,k≠0),这时,y叫做x的正比例函数。
2.一次函数的图像及性质
(1)在一次函数上的任意一点P(x,y),都满足等式:y=kx+b。
(2)一次函数与y轴交点的坐标总是(0,b),与x轴总是交于(-b/k,0)。
(3)正比例函数的图像总是过原点。
(4)k,b与函数图像所在象限的关系:
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小。
当k>0,b>0时,直线通过一、二、三象限;
当k>0,b<0时,直线通过一、三、四象限;
当k<0,b>0时,直线通过一、二、四象限;
当k<0,b<0时,直线通过二、三、四象限;
当b=0时,直线通过原点O(0,0)表示的是正比例函数的图像。
这时,当k>0时,直线只通过一、三象限;当k<0时,直线只通过二、四象限。
二次函数知识点
1.二次函数表达式
(一)顶点式
y=a(x-h)²+k(a≠0,a、h、k为常数),顶点坐标为(h,k),对称轴为直线x=h,顶点的位置特征和图像的开口方向与函数y=ax²的图像相同,当x=h时,y最大(小)值=k。
(二)交点式
y=a(x-x₁)(x-x₂) [仅限于与x轴即y=0有交点时的抛物线,即b²-4ac>0]
函数与图像交于(x₁,0)和(x₂,0)
(三)一般式
y=aX²+bX+c=0(a≠0)(a、b、c是常数)
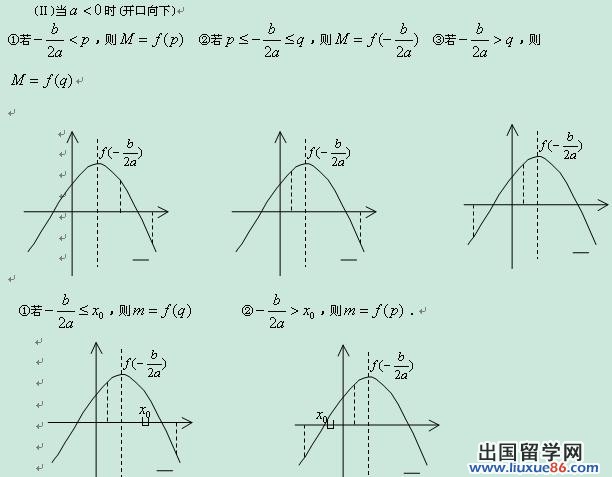
2.二次函数的对称轴
二次函数图像是轴对称图形。对称轴为直线x=-b/2a
对称轴与二次函数图像唯一的交点为二次函数图象的顶点P。
特别地,当b=0时,二次函数图像的对称轴是y轴(即直线x=0)。
a,b同号,对称轴在y轴左侧;
a,b异号,对称轴在y轴右侧。
3.二次函数图像的对称关系
(一)对于一般式:
①y=ax2+bx+c与y=ax2-bx+c两图像关于y轴对称
②y=ax2+bx+c与y=-ax2-bx-c两图像关于x轴对称
③y=ax2+bx+c与y=-ax2-bx+c-b2/2a关于顶点对称
④y=ax2+bx+c与y=-ax2+bx-c关于原点中心对称。(即绕原点旋转180度后得到的图形)
(二)对于顶点式:
①y=a(x-h)2+k与y=a(x+h)2+k两图像关于y轴对称,即顶点(h,k)和(-h,k)关于y轴对称,横坐标相反、纵坐标相同。
②y=a(x-h)2+k与y=-a(x-h)2-...