行测立体几何

　　在考场上人与人拉开差距的除了平常的知识点的积累，还有面对考试题型能够有一个更好的解答思路，下面由出国留学网小编为你精心准备了“行测数量关系技巧：立体几何之立体表面最短路径”，持续关注本站将可以持续获取更多的考试资讯！

行测数量关系技巧：立体几何之立体表面最短路径

　　几何问题在近几年的公职类考试中频频出现，不论是在公务员考试的行测中，还是事业单位联考的职业能力测验中，经常能看到几何问题的身影，尤其是在近几年的国考中，几何问题更是热门考点。几何问题主要测查我们对于平面几何、立体几何的理解以及对相关公式的掌握，其实这些知识在小学和中学就已经是我们所接触学习过的了。所以几何问题的备考，更多地是复习和回顾，做题过程也是公式和方法的应用过程。

　　今天主要来说一下几何问题中的立体表面最短路径问题。立体几何相比较平面几何，不仅需要我们对计算表面积和体积的公式要熟悉，还需要我们有一定的空间想象能力，通过不断练习对图形的把握感要逐渐地强化。立体表面的最短路径问题，就是需要对原来的立体图形作一定地变形，把需要空间想象的立体几何转化为更为清晰直观的平面几何。接下来我们就通过两个例子看一下如何进行转化。

　　例如：一只蚂蚁在棱长为1的正方体的顶点A沿表面爬行到顶点B，那么爬行的最短距离是多少?

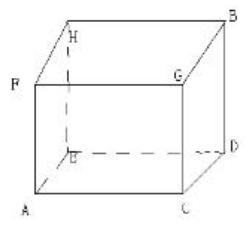
　　我们发现，要想爬行距离最短，尽量朝着B走直线，但在一个立体的表面，这个直线路径该怎么画出来就需要很强的空间想象能力了，更不要说还要计算出来结果。但如果能够把立体几何转化为一个平面几何，题目就变得简单明了了。我们可以把右面的面翻到与正前方的面平齐(或把上方的面翻到与正前方的面平齐)。如下图所示：

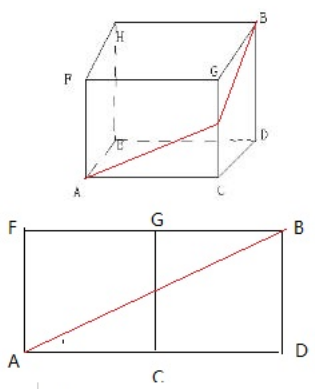
　　通过简单的转换，就可以绕过空间想象，把立体图形转变为简单易解的平面图形，题目也就迎刃而解了。希望通过上面的两个例子，能给同学们一点启发，把握好此类题目的解题方法，通过适当练习，对方法以及几何所涉及的公式都进行练习和掌握，攻克几何问题。

　　推荐阅读：

　　近几年，在国家公务员考试中经常涉及几何问题。在数学运算题型中，几何问题包含两种题型：平面几何问题和立体几何问题。为了便于分析和计算，多数立体几何问题需要转化到平面上进行求解，关注和学习相关的平面几何知识是解决立体几何问题的基础。平面几何知识较为简单，易于掌握，而立体几何问题较为复杂，考生需要掌握更复杂的计算公式和一定的空间想象能力，难度较大。解决此类题型的技巧方法一一详解如下：

　　一、球、圆柱与锥体

　　平面图形通常要计算周长、面积，对立体图形则计算表面积、体积。