行测数量关系答题技巧：工程问题如何设特值

　　行测工程问题怎么解决？小编为大家提供行测数量关系答题技巧：工程问题如何设特值，一起来看看吧！希望大家好好学习答题技巧为考试做准备！

　　行测数量关系答题技巧：工程问题如何设特值

　　在行测考试当中，许多考生只想做一些简单的自己能够驾驭的题型，那么工程问题就在首选之列。这种题型传统，对特值法的依赖较高，所以会熟练应用特值法，就能够解决很多工程问题。特值法比较灵活，因情况不同设法也不同，今天小编就讲解一下在工程问题各种的情况中该如何设特值。

　　一、设什么?

　　工程问题的基本关系式是W=P×t，题目中往往只给出t，结果还是让求t，那么我们就可以设W或t为特值。设的时候是设一推一，而不是同时设。

　　二、怎么设?

　　1. 设W为特值

　　当题目中出现两个以上完成工作总量且中途效率不变的时间时，设“时间们”的最小公倍数为工作总量。

　　例1.一项工程，甲、乙合作 12 天完成，乙、丙合作 9 天完成，丙、丁合作 12 天完成，如果甲、丁合作，则完成这项工程需要的天数是：

　　A.16 B.18 C.24 D.26

　　【答案】B。此题给出的12天、9天、12天三个时间都是完成工作总量且中途效率不变的时间，此时我们设工作总量为 12和9的最小公倍数为36，则甲+乙=3，乙+丙=4，丙+丁=3。因此甲+丁=(甲+乙)+(丙+丁)-(乙+丙)=3+3-4=2。甲、丁合作完成这个工程需要 36÷2=18天。

　　2.设P为特值

　　情况1：当题目中给出或者我们可以推出效率比值时，我们设比值为各自的效率。

　　例2.甲、乙、丙三个工程队完成一项工作的效率比为 2∶3∶4。某项工程，乙先做了三分之一后，余下交由甲与丙合作完成，3 天后完成工作。问完成此工程共用了多少天?

　　A.6 B.7 C.8 D.9

　　【答案】A。题目中已经明确给出，.甲、乙、丙三个工程队完成一项工作的效率比为 2∶3∶4，于是我们设甲、乙、丙的效率分别为 2、3、4，甲丙合作 3 天，完成(2+4)×3=18，则工作总量为 18÷2/3 =27，故乙做三分之一用了 9÷3=3 天，即完成此工程共用了 3+3=6 天。

　　情况2：当团体合作(人数多到不用甲乙丙来表示)时，设每人单位时间内效率为“1”。

　　例3.建筑公司安排 100 名工人去修某条路，工作 2 天后抽调走 30 名工人，又工作了 5天后再抽调走 20 名工人，总共用时 12 天修完。如希望整条路在 10 天内修完，且中途不得增减人手，则要安排多少名工人?

　　A.80 B.90 C.100 D.120

　　【答案】A。此题中工作人数众多，且没有用甲乙丙来表示，我们假设每个工人每天工作量为 1，则这条路的工作量为 100×2+(100-30)×5+(100-30-20)(12-2-5)=800，如果要在 10 天内修完，则要安排 800÷10=80名工人。

　　小编提醒各位考生，掌握住这几种情况中的如何设特值，再遇到工程问题就可以果断拿下了。我们愿用每天的分享助力你的公考之旅!

　　行测数量关系答题技巧：巧用整除

　　提到行测中的数量关系，大家都心里一紧，浮现在脑海的就是耗时间、不会写;但是如果想要行测得到比较高的分数，是不应该存在短板的，那么怎么才能提高效率，节省时间呢?为此小编总结了一种行之有效的巧算方法：整除,帮助大家避开复杂的计算，迅速解题。

　　一、整除的定义

　　整数A/非零整数B=整数C;即A能被B整除。(利用题目中的整除关系来快速判别选项。)

　　例:一袋糠里装有奶糖和水果糖，其中奶糖的颗数占总颗数的3/5.现在又装进10颗水果糖，这时奶糖的颗数占总颗数的3/4。那么，这袋糖里有多少颗奶塘( )

　　A.100 B.112 C.120 D.122

　　【解析】C。题目所求为奶糖的数目，刚开始，奶糖占总的糖果数目的3/5。总的糖果数目为5份，奶糖为3份，不管每一份为多少，奶糖数目为3的倍数，即能被3整除;选择C项。了解了什么是整除之后，接下来我们一起来看看如何快速求解此类问题。

　　二、整除的应用

　　1、文字描述：每、平均、倍数、整除;

　　一个旅游团租车出游，平均每人应付车费40元。后来又增加了7人，这样每人应付的车费是35元，租车费是( )。

　　A.2000元 B.1960元

　　C.1900元 D.1850元

　　【解析】B。由题意可知，租车费是35的倍数，35=5×7，因此租车费应是7的倍数，选项中只有B符合。

　　2、数字描述：比例、分数、百分数(需化为最简比);

　　学校有足球和篮球的数量比为8∶7，先买进若干个足球，这时足球与篮球的比变为3∶2，接着又买进一些篮球，这时足球与篮球数量比为7∶6。已知买进的足球比买进的篮球多3个，原来有足球多少个?

　　A.48 B.42 C.36 D.30

　　【解析】A。由“足球和篮球的数量比为8∶7”可知足球的数目应为8的倍数，选项中只有A项符合。

　　三、整除在真题中的应用

　　例题1：某俱乐部中女会员的人数比男会员的一半少61人，男会员的人数比女会员的3倍多2人，问该俱乐部共有会员多少人?

　　A.476人 B.478人

　　C.480人 D.482人

　　【解析】D。“男会员的人数比女会员的3倍多2人”说明会员总数减2能被4整除，由此排除选项A、C;“女会员人数比男会员的一半少61人”说明总会员数加61能被3整除，由此排除B。

　　例题2：某单位有工作人员48人，其中女性占总人数的37.5%，后来又调来女性若干人，这时女性人数恰好是总人数的40%，问调来几名女性?

　　A.1人 B.2人 C.3人 D.4人

　　【解析】B。根据题意，最终女性人数是总人数的2/5，则最后总的职工数应是5的倍数，原有职工48人，结合选项，只有加入2名女性职工才能满足题意。

　　行测数量关系模拟题及答案

　　行测科目中的数量关系一直是考生们比较头疼的部分：一是难，不会做;二是时间紧，没空看。其实主要原因还是考生们没有掌握住数量关系的答题方法，今天教育专家就来通过几道经典题目进行解析，希望能带给大家柳暗花明又一村的感觉。

　　1.某班同学共有50人，其中一部分参加学校运动会，报名参加乒乓球比赛的有27人，报名参加短跑的有25人，报名参加接力赛的有21人，已知每个人最多参加两项比赛，那么班里最多有多少人没有报名参加运动会?()

　　A.14 B.13 C.12 D.11

　　【点拨】本题属于容斥问题，但也涉及到极值问题，两个考点杂糅在一起，这种考察形式在省考中很常见。解决容斥问题常用的方法是文氏图法和公式法，解题原则：不重复，不遗漏，多层变一层。

　　【解析】B。公式法，设参加一项比赛的人数为a，参加两项比赛的为b，参加三项比赛的为c，一项都不参加的为d，根据条件有：a+b+c+d=50，a+2b+3c=27+25+21=73，c=0，求d的最大值，想要d尽可能大，a+b的值尽可能小，a+2b=73，因此a=1，b=36，所以d=13，根据答案为B。

　　2.在一个不透明的箱子里，放有3个黄球，4个红球，2个蓝球，这些球除了颜色之外，球的大小，材质等都一样，现要求从中摸出5个球，请问红球最多且黄球个数不少于蓝球的有多少种?

　　A.30 B.50 C.60 D.120

　　【点拨】本题属于排列组合，需要用到分类分步思想，这类题型在省考中属于难题，根据“红球最多，黄球个数不少于蓝球”这句话可以把问题分为两大类分别求解，即2个红球，2个黄球，1个蓝球;3个红球，1个黄球，1个蓝球。

　　4. 经理给当天18名工人发完工资后，把总钱数写在一张纸上，回家后跟儿子玩耍，儿子不小心把纸撕坏了，纸上只剩5□5□，现在只知道每名工人的工资都一样，而且是整数元。问：每名工人当天的工资最高可能是()

　　A.314 B.325 C.331 D.336

　　【点拨】本题属于计算问题，在省考中出现的频率较高;由于题干条件有限，无法直接计算，所以只能采用带入排除或者根据题干中涉及到的“整数元”这个信息，借助于整除思想来找到突破口。

　　【解析】C。方法一：因为问的是工资最高为多少，所以从大的选项开始代入，哪个选项代入进去满足选项乘以18最后得到的数字是5□5□，即为正确答案，故本题答案选C。

　　方法二：要想保证每人的工资最高，在总人数一定的情况下，只要保证总工资最多就行。根据题干可知总的工资一定能被18整除，18的整除判定拆分之后变成2和9的整除判定，即5□5□一定能同时被2和9整除。被2整除要求最后一位是0、2、4、6、8，被9整除要求所有数字之和能被9整除，现有的数字之和是10要想能被9整除，还得尽可能大，剩下的数字之后最大是17，即这两个□一个是8一个是9，再结合2的整除，只能最后一个□是8，故总工资最多是5958，每人的工资最多是5958/18=331，本题答案选C。

　　5.某单位共有职工72人，年底考核平均分数为85分。根据考核分数，90分以上的职工评为优秀职工，已知优秀职工的平均分数为92分，其他职工的平均分数是80分，问优秀职工的人数是多少?

　　A.12 B.24 C.30 D.42

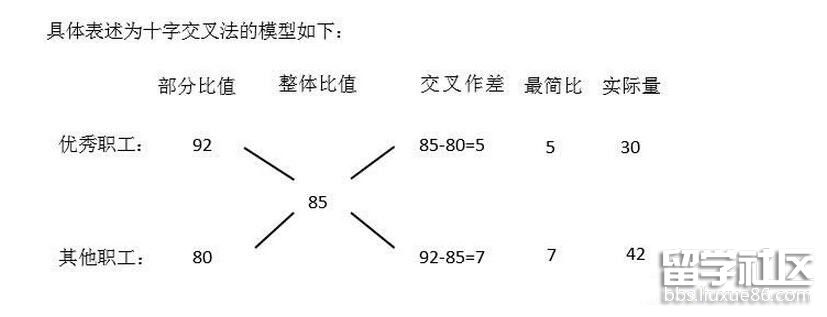
　　【点拨】本题属于盈余亏补问题;优秀员工与非优秀员工混合就正好是全体员工，题目分别有优秀员工平均分，非优秀员工平均分，全体员工平均分，符合平均数混合问题，可以采用十字交叉法。

　　【解析】与全体员工平均分相比，平均每个优秀职工比全部职工高92-85=7分，平均每个非优秀职工比全部职工低85-80=5分。平均每个盈余和亏损的比例为7:5，盈余和亏损的量总量应该相等，所以优秀职工与非优秀职工的比例为5:7，一共12份，全体职工一共72人，所以每份6人，所以优秀职工有5×6=30人。