在考场上人与人拉开差距的除了平常的知识点的积累,还有面对考试题型能够有一个更好的解答思路,下面由出国留学网小编为你精心准备了“行测数量关系技巧:和定最值解题技巧”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:和定最值解题技巧
众所周知,和定最值问题是公务员考试当中的一个常考考点,所以学会如何巧解和定最值问题就尤为重要。首先,在众多数量关系题目中,我们要先学会识别出哪些题型考的是和定最值,因此,我们就需要知道和定最值问题的题型特征。和定最值问题指的是几个数的和一定,求其中某个量的最大或最小值问题。因此我们就提炼出了和定最值问题的题型特征:和一定,求某个量最大或最小值。而在和定最值,常见考点主要有3种类型:同向极值、逆向极值以及混合极值。今天主要来介绍一下逆向极值的巧解方法。
首先要想更好地解决逆向极值问题,我们需要先带着大家回忆一下一些与解题相关的知识点。我们知道对于等差数列的求和,有一个常用的一个求和公式叫做中项法求和公式。

逆向极值主要是指求最大量的最小值或者是求最小量的最大值。接下来,我们来看一下逆向极值的例题:
【例1】某公司有7个部门,共有56人,每个部门的人数互不相等,已知技术部人数最多。问技术部最少有多少人?
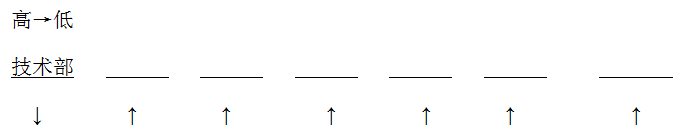
【解析】:此题求的是部门最多的技术部人数最少有多少人,因此想让技术部门人数最少,就应该让其他部门人数尽可能多,但再多也不能比技术部门的人多,只能无限地接近于技术部门的人数(尽量将总人数均分),因此对于第2,3,4,5,6,7这6个部门的人数依次比前一项少1,所以这些部门的人数形成了一个等差数列,我们先求出7个部门的平均数为56÷7=8=中间项,因此我们根据这个平均数构造上述数列,可得
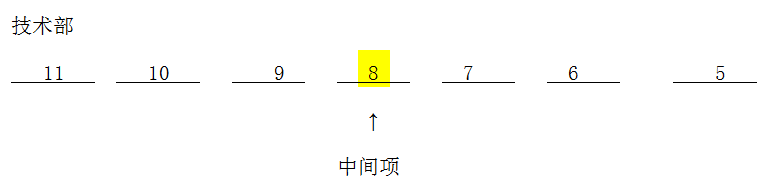
则所求为11人,即技术部最少有11人。
【例2】现有100块糖,把这些糖分给10名小朋友,每名小朋友分得的糖数都不相同,则分得数量最多的小朋友至少分得几块糖?

【解析】:在和定最值问题当中,我们一般习惯性从大往小以此写数,此题求的是分得数量最多的小朋友最少分得几块糖,因此想让分得数量最多的小朋友分得的糖数尽可能少,就应该让其他小朋友分得的糖数尽可能的多,但再多也不能比分得数量最多的小朋友多,只能无限地接近于分得数量最多的小朋友的糖数(尽量将总糖数均分),因此对于第2,3,4,5,6,7,8,9,10这9个部门的人数依次比前一项少1,所以这些部门的人数形成了一个等差数列,因此我们先求出10名小朋友平均分得的糖数为100÷10=10=中间两项之和÷2,因此我们根据这个平均数构造上述数列,可得
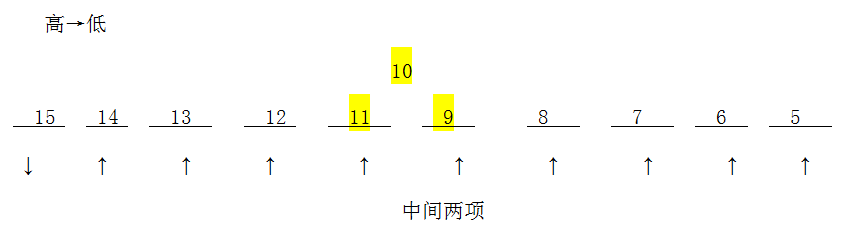
即分得数量最多的小朋友最少分得15块糖.
推荐阅读:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |