做了许多行测模拟题还是没有有效的提升自己的分数?那是你没有掌握一些技巧和重点,下面由出国留学网小编为你精心准备了“行测数量关系技巧:和定最值问题6.4”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:和定最值问题6.4
今天就由小编来带大家认识和学习数量关系中比较难的一类题,叫做和定最值问题,我们先来看一道例题。
例题.现有29个N95口罩分给五个人,已知每个人都分到口罩并且数量互不相同,这五个人中有一位是医护人员,所以要把口罩尽可能多地分给他,问他最多能分到多少个口罩?
A.15 B.16 C.19 D.25
【答案】C。解析:这道题目中我们知道口罩的总数是一定的,而医护人员分得的口罩要尽可能多,则其他人分得的口罩数要尽可能小,而题干中又有条件要求每人都分到并且数量互不相同,不妨我们按照分得口罩数由多至少排序并标号,把这五个人表示出来。第一个人分得最多,具体是几不清楚,我们先设作x,而分得最少的第五人要分到口罩,最少为1,第四人比第五人要多,而他的口罩数也要尽可能小,则为2,同理第三人和第二人分得口罩数为3和2。这时五个人的口罩数都已表示出来,而总数为29,可以得到x+4+3+2+1=29,解得x=19,选C。

通过这道例题大家应该对和定最值问题有了一定的认识,这类题的特点就是几个量的和一定,让我们求某个量的最大值或最小值,而我们的做法就是按照从大到小对这几个量排序,然后分析出每个量的取值,再利用每个量加起来等于总和,求解出我们想要的答案。
一、题型特征:已知几个量和一定,求某个量的最大值或最小值。
二、解题原则:1、求某个量的最大值,则让其他量尽可能小。
2、求某个量的最小值,则让其他量尽可能大。
三、例题展示:
例1.8名工人在流水线工作,一个小时共完成零件183个。已知每名工人的工作效率互不相同,且效率最快的工人一小时完成了27个零件,则效率最慢的工人一小时最少完成几个零件?
A.15 B.17 C.20 D.21
【答案】A。解析:完成零件总数一定,效率最慢的工人一小时完成的零件要最少,则其他人完成要尽可能多,我们可以按照完成效率由快到慢的排序表示,最慢的人做多少个不知道,我们可以设为x,最快的人完成27个,第二快的人要比他慢,但又要尽可能地大,所以为26,同理第三、四、五、六、七个人一个小时所做零件数依次为25、24、23、22、21个,这样我们就把每个人的一小时所做零件数表示出来了,他们一小时共做183个零件,可以得到28+27+26+25+24+23+22+21+x=183,求解得到x=15,选A。

例2.某高校要从7个专业抽调256人组成一个方阵,7个专业因为总人数不同,抽调的人数互不相同,则抽调人数最多的专业最少抽调了多少人?
A.39 B.40 C.41 D.42
【答案】A。解析:抽调总人数是一定的,抽调人数最多的专业所抽出的人数要尽可能少,则其他专业抽调的人数就要尽可能多,我们可以按照抽调人数从多到少的排序表示,抽调最多的专业抽了多少人不知道,我们可以设为x,抽调第二多的专业人数要尽可能多,但又不能等于x,所以为(x-1),同理我们可以表示出其他专业抽调人数,各专业抽调人数和为256,可以得到x+x-1+x-2+x-3+x-4+x-5+x-6=256,我们可以求出来x≈39.4,而x代表的是人数,最大也只能取39.4,所以取整应为39,选A。

行测数量关系备考:让我们的思维回归
在学习数量关系这一部分的时候是不是有时候有这种感觉?似乎脑海中千万方法呼啸而过,但是只有个影子,感觉哪个都似是而非,不知道从何处做起。那这个时候就该让大脑减减负了,让自己的思维放松,回到最初的时候——你会发现,方程法才是你的本命大法。是的,好方法千千万,奈何一到题场就失散,到最后靠方程来翻盘。这是保命法典,一定要学好,学到炉火纯青,做到信手拈来。今天小编就给大家说说方程法解题的关键。
(1)首先,你得确定这个题是方程大法能搞定的。
对的方法遇到对的题,才能顺风翻盘,否则只会粉身碎骨。所以,在决定思维“偷懒”之前和题目确定一下眼神,看看是不是对的台本。判定规则很简单,只用看看题目里是不是存在等量关系。
等量关系有两种,一明一暗。一种是题目明确给出的,一般来说是计算关系,在看题目信息的时候要注意,比如“共”、“倍”、“多”、“少”等等描述数据间计算关系的词要重点关注;另一种是题目没有直接给出,需要自己结合题目考点去联想的,找这种等量关系要求大家熟记公式。
(2)其次,即使同样是方程法,方程难度也有青铜和王者的区别。
千万别确定能用方程法就掉以轻心,未知数设置不恰当,方程式列复杂了,都有可能让你分分钟怀疑人生。
①设未知数,所设的量建议小一点,与其他量关系要密一点。别太浪,千万别数据关系都没搞清楚就瞎设未知数,建议仔细看题让自己冷静下来。设未知数的方式千千万万,最后比较好使的就三种:第一种设最直接的,求什么就设什么,解出来就是答案,不担心做对而选错,适合所求为基础量的题目;第二种,设题目中最小的量,这样一来表示其他的量时大片加法或乘法,避免出现太多分式加大了解方程的难度,这种设未知数的方法演化的一类情形就是题目里直接给出比例关系了,那就直接按照比例关系设未知数,比如甲:乙=4:3,那就直接设甲和乙分别为4x、3x;第三种,设与其他量关系密切的量,方便表达参与计算的其他量,简化所列方程。
②列方程,建议要有大局观。在公考数量关系题目当中,如果设未知数恰当了,但是最后方程列出来极其复杂且很难求解,大部分原因在于对题目中的等量关系处理不合理。在使用等量关系列方程时,要有大局观,做到“抓大放小”。一般选择部分间的等量关系来表达其他量,用更大的整体间的等量关系列方程时会比较直接,且可以避免出现过于复杂的方程。
(3)最后,即使方程一样,一不小心也有可能慢人一步。
很多考生列完方程就埋头苦“解”。这样做的后果是,很容易给自己加解题步骤和解题难度——因为有时候,题目所求未必需要完全解出方程。因此,为了避免出现这种情况,建议大家列完方程后,确定一下题目所求为何,是否需要完全解出方程。
只要功夫深,基本大法也能成神。如果感觉自己对众多新的解题方法无所适从时,你不妨试试苦练基本功,多领悟方程法。一方面,为自己解题“保底”,另一方面方程法是其他解题方法的根本,练好方程法也有助于理解其他解题方法。
行测数量关系技巧:数学马拉松之行程问题
在公务员、企事业单位、军队文职等各类考试中,有一类很重要的题型,那就是行程问题。小编通过对历年考试题目进行剖析,发现行程问题的常见题型包括三大类:普通行程问题、相遇追击问题、流水行船问题。接下来小编为各位考生介绍三种题型。
例题1:一列火车通过一条长1140米的桥梁(车头上桥至车尾离桥)用50秒,火车穿越长1980米的隧道用80秒,则这列火车车身是( )米。
A.260 B.270 C.360 D.380
【答案】A。解析:行程问题基本关系式为:路程=速度×时间。火车的速度为(1980-1140)÷(80-50)=28米/秒,火车的车身是50×28-1140=260米。
例题2:一支600米长的队伍行军,队尾的通讯员要与最前面的连长联系,他用3分钟跑步追上了连长,又在队伍休息的时间以同样的速度跑回了队尾,用了2分24秒。如队伍和通讯员均匀速前进,则通讯员在行军时从最前面跑步回到队尾需要多长时间?
A.48秒 B.1分钟 C.1分48秒 D.2分钟
【答案】D。解析:根据题意可知,通讯员的速度为
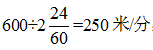
,通讯员用3分钟追上连长,此过程为追及过程,追及过程的基本关系为:路程差=速度差×时间。则通讯员与队伍行军速度的差为600÷3=200米/分,则队伍行军速度为250-200=50米/分;通讯员在行军时从最前面跑回队尾为相遇过程,相遇过程的基本关系为:路程和=速度和×时间,因此所需要的时间为600÷(50+250)=2分钟。故本题选D。
例题3:甲、乙两港相距720千米,轮船往返两港需要35小时,逆流航行比顺流航行多花5小时;帆船在静水中每小时行驶24千米,问帆船往返两港要多少小时?
A.58小时 B.60小时 C.64小时 D.66小时
【答案】C。解析:流水行船问题中,船速=(顺水速度+逆水速度)÷2;水速=(顺水速度-逆水速度)÷2。由题目可知轮船逆流航行了20小时,顺流航行了15小时。可得水流速度是(720÷15-720÷20)÷2=6千米/小时,所以帆船顺水速度是24+6=30千米/小时,逆水速度是24-6=18千米/小时,往返需要720÷30+720÷18=64小时。
推荐阅读:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |