水滴石穿、汇流城河,任何的事情都是非一日便成功的,是需要长时间的积累,下面由出国留学网小编为你精心准备了“行测数量关系技巧:巧用整除思想快速解决行测问题”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:巧用整除思想快速解决行测问题
各位考生,对于公务员考试行测科目来说,做题速度是永远的主题,而行测理一直是大部分考生所头疼的部分,现在的公务员考试越来越难,但也有部分的题可以利用一些秒杀的技巧来巧解,这样就可以为我们节省下大量的时间。而今天所要谈到的整除思想就是技巧之一。
一、定义
整数÷整数=整数
二、应用环境
1、文字描述出现“每”、“平均”、“倍数”等字眼可以考虑整除思想。
2、数据出现“分数”、“百分数”、“比例”、“小数”这些形式时考虑整除思想。
三、例题应用
例1.某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人,问今年男员工有多少人?
A.329 B.350 C.371 D.504
【答案】A。
解析:方法一、方程求解:方程是解决行测理问题常用的方法,好用但是有些费时。可以设去年男员工X人,则去年女员工为(830-X)人,94%X+105%×(830-X)=833,解得X=350,那么今年男员工的人数为350×94%=329。这个方程比较复杂,解的过程耗费时间较多。
方法二、整除思想来解:题目当中出现了百分数,所以可以用整除思想来解。今年男员工的人数是去年的1-6%=94%,总人数一定含有因子47,即总人数能够被47整除,这时验证4个选项,只有A选项能够被47整除,所以选择A选项。
是不是很惊喜呀?用整除的一些办法来解决咱们行测理得题目的话很快就可以了,那么我们再来看几道题进行一下巩固。
例2.小雪和小敏的藏书册数之比是7:5,如果小雪送65本给小敏,那么他们的藏书册数之比是3:4,则小敏原来的藏书是多少册?
A.175 B.245 C.420 D.180
【答案】A。
解析:他们的藏书册数之比是3:4,就意味着小敏原来的书的册数加上65之后能被4整除,则只有选项A满足题意。
例3.某粮库里有三堆袋装大米,已知第一堆有303袋大米,第二堆有全部大米袋数的五分之一,第三堆有全部大米袋数的七分之若干。问粮库里共有多少袋大米?
A.2585 B.3535 C.3825 D.4115
【答案】B。
解析:这道题如果用其他的方法可能很难快速得出答案,显然用整除思想就很快解决问题,因为总的大米袋数一定可以被5和7整数,所以说,只有B选项符合。
通过对于定义以及应用环境的了解,并且经过几道例题的练习,相信各位同学对于整除都有了新的理解,在考场上巧用整除技巧,可以更快的解决问题,提升做题速度,使我们的成绩更上一层楼。
行测技巧:数学运算之一题多解
众所周知,行测数量关系是大部分考生的“拦路虎”。很多考生基本上谈虎色变,所以遇见这类问题要么没时间做,要么干脆放弃。2020省考已经日渐临近,考生们此时要多学各种快速解题技巧。接下来就如何对于数量关系一题多解进行详细的介绍,考生可以根据自己的实际备考情况和能力,选取适合自己的解题方法
例1:小李的弟弟比小李小2岁,小王的哥哥比小王大2岁、比小李大5岁。1994年,小李的弟弟和小王的年龄之和为15岁。问2014年小李和小王的年龄分别是多少?
A 25,32 B27,30 C30,27 D32,25
解法一:本题考查的是年龄问题结合方程。设小李的年龄为X,则李弟为X-2,王哥为X+5,小王的年龄为X+3。可以得到方程为:(X+3)+(X-2)=15,易知X=7,即小王年龄为7岁,小王年龄为10岁,2014年两人分别为27和30.故答案为B选项。
解法二:本题我们只需要关注题干中的一个条件“小王的哥哥比小王大2岁、比小李大5岁”,可知小王的年龄比小李要大。故可排除CD选项,并且也能知小王比小李大3岁,故最终答案为B选项。
例2:某公司计划采购一批电脑,正好赶上促销期,电脑打9折出售,同样的预算可以比平时多买10台。问公司的预算在平时可以买多少台电脑?
A. 60 B. 70 C. 80 D. 90
解法一:本题考查利润问题采用特值法并结合方程。假设电脑在平时的价格为100元,促销期打九折单价为90元,假设平时可采购电脑为X台,则促销期采购台数为X+10根据预算相等可以得到方程:100X=90(X+10),得X=90。故答案为D选项。
解法二:比例法。根据预算相等,符合M=A×B,单价和数量成反比,平时和促销期的单价比为10:9,则易知采购数量平时和促销期比为9:10,差了一份所对应的实际量为
10台,故平时9份为90台,同样也能得到答案为D选项。
解法三:比较构造法。方案一:公司预算采购100元单价的电脑采购完,无剩余;方案二:同样的预算如果按照平时的采购台数,则还能采购10台,按照现有的单价算即余下10×90=900元,故之前的台数=900÷(100-90)=90台。
解法四:不定方程。假设平时采购台数为X台,促销期采购台数为y台。则可以得到方程为100X=90y,X、y为整数解,故X必能被90整除,结合选项只能选择D选项。
通过以上几道题目各位考生会发现,数量关系往往存在一题多解的情况,解题的难易程度也取决于选择的解题方法。希望大家能够理解并深入探究数量关系,那么等待你们的就是在行测数量关系中多拿几分。
行测备考技巧:随机模型下的“古典概率”
概率问题是行测考试数量关系中经常出现的一类题型,概率问题让很多考生“望而生畏”。其实概率问题,可谓是“会者不难,难者不会”,有些考生甚至分不清楚题目难易,干脆一股脑放弃了。鉴于这种情况,接下来将为各位考生分享一下随机模型下的概率问题。
一、基础知识
“概率”也称作“或然率”,它表示随机事件发生的可能性大小。
常考题型:古典概率,其特征是:①随机试验中所有可能出现的基本事件是有限的;②每一个基本事件出现的可能性是相等的。即一次试验由n个基本事件组成,每个基本事件发生的可能性是相同的,若事件A包含m个基本事件,则定义事件A发生的概率为
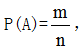
也就是事件A发生的概率等于事件A所包含的等可能样本数除以总事件所包含的等可能样本数。
二、例题展示
例:某娱乐节目中有一个抽奖环节,抽奖箱中有三张奖券,其中只有一张一等奖,甲、乙、丙三个人按照先后顺序无重复抽取一张奖券,那么此次游戏,甲、乙、丙抽到一等奖的概率是否相同呢?

【解析】:随机模型下,甲、乙、丙抽到一等奖的概率与抽取顺序无关,都是相等的。
所以遇到随机模型下的概率问题,我们就不用再逐个去分析,无论求第几个人选中的概率都是相等的,我们都可以借助第一个人抽到的概率求解,从而简化问题,快速找到答案。
推荐阅读:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |