行测朴素逻辑备考：巧用确定性和关联性信息

　　想要更好的通过公务员行测考试，掌握行测考试技巧很重要，下面由出国留学网小编为你准备了“行测朴素逻辑备考：巧用确定性和关联性信息”，仅供参考，持续关注本站将可以持续获取更多的内容资讯！

行测朴素逻辑备考：巧用确定性和关联性信息

　　历年来行测必然性推理中的朴素逻辑都是重要考点。很多同学遇到这种题都无从下手，不知道怎样找信息。朴素逻辑中常用的解题的入手点是：确定性信息和关联性信息。何为确定性信息?即相对来说情况数比较少的信息。何为关联性信息?即题干中出现次数比较多的信息。接下来通过几道题目和小编一起来看看如何应用。

　　【例1】甜品店有四种甜点：双皮奶、布丁、蛋糕和冰淇淋。B比A贵，C最便宜，双皮奶比布丁贵，蛋糕最贵，冰淇淋比D贵。

　　关于这四种甜点，下列说法正确的是：

　　A. A是双皮奶，B是蛋糕，C是冰淇淋，D是布丁

　　B. A是布丁，B是冰淇淋，C是蛋糕，D是双皮奶

　　C. A是冰淇淋，B是蛋糕，C是布丁，D是双皮奶

　　D. A是冰淇淋，B是蛋糕，C是双皮奶，D是布丁

　　【答案】C。

　　【解析】根据题干信息，C最便宜和蛋糕最贵是最确定的。进而可知双皮奶不是C，蛋糕不是C，冰淇淋不是C，所以只能布丁是C，结合选项排除，正确答案是C。

　　【例2】A、B、C、D四个女生住在同一个宿舍，她们当中有一个人在洗水果，一个人在画画，一个人在上网，一个人在复习功课。其中：

　　(1)A不在洗水果，也不在复习功课

　　(2)B不在上网，也不在洗水果

　　(3)如果A不在上网，那么D不在洗水果

　　(4)C不在复习功课，也不在洗水果

　　(5)D不在复习功课，也不在上网

　　下列说法正确的是：

　　A.B在复习功课，C在画画 B.C在洗水果，D在复习功课

　　C.A在上网，B在画画 D.A在复习功课，D在画画

　　【答案】A

　　【解析】根据洗水果出现次数最多，判断出A、B、C不洗水果，可知D洗水果，结合选项，排除B、C选项。根据复习功课出现三次，可知B复习功课，排除D，正确答案A 。

　　行测图形推理技巧：对称性的“变”与“不变”

　　提到对称性，我们会想到两种对称：中心对称和轴对称。这是我们从小就接触的内容，大家对此并不陌生。其中，中心对称情况相对单一，而轴对称情况比较多变。在行测图形推理中，轴对称常常会考查两个方面的规律：一个是对称轴的数量，即图形有几条对称轴;另一个是对称轴的方向，即竖直、水平或倾斜。接下来，我们通过几个例题来感知一下“对称轴”的常规考法。

　　【例题1】把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：

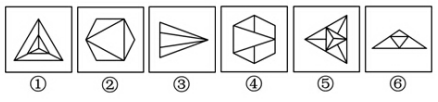
　　A.①⑤⑥，②③④ B.①③⑤，②④⑥

　　C.①②③，④⑤⑥ D.①②⑤，③④⑥

　　【解析】D。题干图形就自身特点而言，较为规则，可以考虑图形的对称性。观察题干，可以看到所有图形都是轴对称图形，由于对称轴的数量与方向是我们常考的考点，因此可以从“对称轴”入手进行解题。其中，①②⑤均为三条对称轴，③④⑥均为一条对称轴。所以本题选D。

　　【例题2】从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：

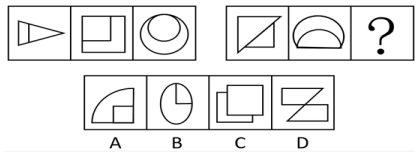
　　【解析】C。观察题干，可以发现题干中图形也较为规则，都是轴对称图形。此时，我们同样可以考虑对称性常考的考点，即对称轴的数量与方向。题干中图形均有一条对称轴，但方向不同。左侧三个图形的对称轴方向分别为水平、倾斜、竖直，整体上呈现依次顺时针旋转45度的变化规律。右侧图形的对称轴方向按相同规律变化，所以本题选C。

　　通过这两个题我们可以大致了解对称性这一知识点的考查形式，这也提示我们在观察到一个图形具有对称性这一特点时，要能够快速地想到中心对称和轴对称这两种规律。但仅仅想到还不够，近几年命题更加灵活、新颖，对称性的考查也不仅仅局限于以上情况，而是有创新性变化。我们一起来看下面这道例题。

　　【例题3】从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：

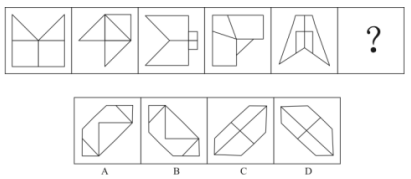
　　【解析】B。通过观察，可以看到题干中图形都是轴对称图形，然后看是否是轴对称的常考考点：对称轴的数量和方向。题干中的图形，对称轴方向依次顺时针旋转45度，据此可排除A、C两项。进一步观察题干所给图形，其中奇数项图形的对称轴均与图形中的一条线重合，而偶数项图形不重合。所以本题选B。

　　综上，我们可以窥见行测图形推理中关于对称性的偏爱以及命题中的创新性变化。然而，万变不离其宗，我们在平时的练习中要注意思考和总结，立足于对称性的基础上，紧跟命题变化，大胆假设，小心求证，把握对称性的“变”与“不变”。

　　行测数量关系技巧：巧解鸡兔同笼问题

　　行测备考过程中，除了多多刷题之外，更重要的是要掌握一定的解题技巧，技巧是提升做题速度的一大法宝。行测数量运算部分一直是考生认为难度最大的一个板块，通常准确率难以达到50%，甚至是花费了大量的时间来做该部分。那么原因主要还是大家对这部分题目有着畏怯的心理，未战先败;另外的原因就是在做这一部分题目的时候缺乏相应的方法和技巧，导致浪费了大量的时间在一些所谓的难题上。

　　今天教育专家就和大家介绍一个比较实用的解题技巧——鸡兔同笼。我们先来看一道经典例题：

　　【例题】在一个笼子里养了鸡和兔两种动物，从上面数头共35个，从下面数脚共94个，问笼中鸡兔各几只?

　　解法一：方程法

　　设鸡、兔各有x, y只

　　根据等量关系头共35和脚共94可以得到x+y=35;2x+4y=94.

　　这样可以得到x=23, y=12

　　解法二：鸡兔同笼思想

　　可将笼中动物全部看成鸡(兔也可)，这样35只鸡有35个头和70只脚，会发现脚的数量还差24只。之所以脚的数量对不上，是因为其中的一些兔子被当成了鸡，一只兔子看成一只鸡，就少掉2只脚，所以一共少了24只脚，就对应把12只兔子看成了12只鸡。因此就得到了兔子的数量为12，所以鸡的数量就为23。

　　通过比较这两种方法，可以看出第二种方法(鸡兔同笼思想)相对于基础的方程法解题更快，熟悉这种方法后甚至可以达到口算的效果。那么我们接下来就来总结下鸡兔同笼问题的题目题型特征和解题方法。

　　题型特征：存在两个总量(一共35个头，一共94只脚);存在两个分量(一只鸡有2只脚，一只兔子有4只脚)

　　鸡兔同笼思想：

　　如果先设的是鸡，求出来的是兔子;如果先设的是兔子，则求出来的鸡。简单说也就是：设鸡求兔，设兔求鸡。

　　【小试牛刀】某餐厅设有可坐12人和可坐10人两种规格的餐桌共18张，最多可容纳208人同时就餐，问该餐厅有几张10人桌?

　　A.2 B.4 C.6 D.8

　　【答案】B。解析：题干中出现了以下的题型特征，两个总量(一共18张桌子，一共可坐208人)，两个分量(一桌可坐12人，一桌可坐10人)，所以我们可以直接利用鸡兔同笼模型解答。设全为12人桌，则共12×18=216人，实际上只有208人，所以(216-208)/(12-10)=4为所求，故选B。

　　行测数量关系备考：“发挥特长”搞定合作问题

　　所谓多劳力合作问题是指多个人合作完成工作时，研究在工作量一定情况下花费时间最少或时间一定情况下产出最大化的问题，此类问题解题的关键点是尽可能发挥合作者各自的优势。此类题型一共有两种考法，分别为已知效率关系和已知时间关系，我们先来学习已知效率关系的题型。

　　例1：某快餐店的一号餐是炸鸡和薯条各一份，王华和周敏是这家快餐店的外卖配餐员，王华每10分钟可以生产炸鸡18份或薯条28份，周敏每10分钟可以生产炸鸡17份或薯条32份。则如果要配160份一号餐，最少需要多少分钟?

　　A.70 B.84 C.96 D.100

　　第一步，根据效率判断优势。(时间以10分钟为单位)

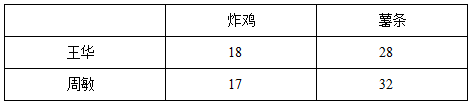
　　根据表格不难判定，王华生产炸鸡效率大，周敏生产薯条效率大，所以王华优先生产炸鸡，周敏优先生产薯条。

第二步，根据效率判断各自完成情况。因为王华每10分钟生产炸鸡18份，周敏每10分钟生产薯条32份，炸鸡总量和薯条总量相同，所以周敏生产160份薯条需要分钟，此时王华生产薯条炸鸡份，少70份。第三步，计算剩余量完成时间。此时王华周敏一起生产70份炸鸡，时间为分钟。

　　第四步，计算完成时间。50+20=70分钟，所以选择A。

　　例2:甲和乙手工制作一种工艺品，每件工艺品由一个A部件和一个B部件组成。甲每天可以制作150个A部件，或者制作75个B部件;乙每天可以制作60个A部件，或者制作24个B部件。现两人一起制作工艺品，10天时间最多可以制作多少该工艺品?

　　A.660 B.675 C.700 D.900

　　解决此类题分以下步骤。

　　第一步，根据效率判断优势。

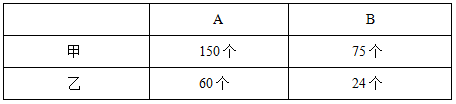
　　观察可知甲完成A和B效率都比乙大，但是甲更擅长做哪份工作呢?

由于，说明甲完成1个B的时间可以完成2个A;，说明乙完成1个B的时间可以完成个A，,说明乙相对来说完成A效率更大，乙更擅长A，甲更擅长B，因此优先安排乙做A，甲做B。第二步，根据效率判断各自完成情况。甲每天完成75个B，乙每天完成60个A，明显相同时间内甲完成的任务量更多。要使A和B总量一样多，则10天时间乙只做A，可以完成600个A，而甲完成600个B仅需要。甲还剩余2天时间，此时甲乙共完成600件工艺品。第三步，计算剩余时间完成量。甲剩下的2天时间部分时间做A，部分时间做B，由于A和B量要相同，效率是150:75=2:1，则时间为1:2，即用天做A，其余天做B。因此甲可以完成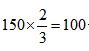个A，同时其余时间能对应完成100个B。此时又完成100件工艺品。