不等式与不等式组
【课标要求】 考点 课标要求 知识与技能目标 了解 理解 掌握 灵活应用 一元一次不等式(组) 理解并掌握不等式的性质,理解它们与等式性质的区别 ∨ ∨ ∨ 能用数形结合的思想理解一元一次不等式(组)解集的含义 ∨ ∨ ∨ 正确熟练地解一元一次不等式(组),并会求其特殊解 ∨ ∨ 能用转化思想、数形结合的思想解一元一次不等式(组)的综合题、应用题 ∨ ∨ ∨
【知识梳理】
1.判断不等式是否成立:关键是分析判定不等号的变化,变化的依据是不等式的性质,特别注意的是,不等式两边都乘以(或除以)同一个负数时,要改变不等号方向;反之,若不等式的不等号方向发生改变,则说明不等式两边同乘以(或除以)了一个负数。因此,在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。
2.解一元一次不等式(组):解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是,不等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质。一元一次不等式(组)常与分式、根式、一元二次方程、函数等知识相联系,解决综合性问题。
3.求不等式(组)的特殊解:不等式(组)的解往往是有无数多个,但其特殊解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集, 然后再找到相应的答案。注意应用数形结合思想。
4.列不等式(组)解应用题:注意分析题目中的不等量关系,考查的热点是与实际生活密切相联的不等式(组)应用题。
考查学生对知识的掌握,灵活运用知识的解题的能力,同时考查学生数学建模的能力。
【能力训练】
一、填空题:
1.用不等式表示:① a大于0_____________; ② 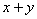 是负数____________; ③ 5与x的和比x的3倍小______________________。
是负数____________; ③ 5与x的和比x的3倍小______________________。
2.不等式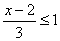 的解集是__________________。
的解集是__________________。
3.用不等号填空:若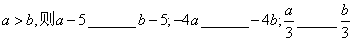 。
。
4.当x_________时,代数代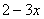 的值是正数。
的值是正数。
5.不等式组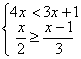 的解集是__________________。
的解集是__________________。
6.不等式![]() 的正整数解是_______________________。
的正整数解是_______________________。
7.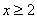 的最小值是a,
的最小值是a,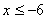 的最大值是b,则
的最大值是b,则
8.生产某种产品,原需a小时,现在由于提高了工效,可以节约时间8%至15%,若现在所需要的时间为b小时,则____________< b <_____________。
9.编出解集为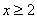 的一元一次不等式为______________________。
的一元一次不等式为______________________。
10.若不等式组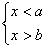 的解集是空集,则a、b的大小关系是_______________。
的解集是空集,则a、b的大小关系是_______________。
二、选择题:
11.下列不等式中,是一元一次不等式的是( )
A.2x-1>0 B.-1<2 C.3x-2y<-1 D.y2+3>5
12.不等式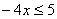 的解集是( )
的解集是( )
A.x≤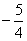 B.x ≥
B.x ≥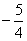 C.x≤
C.x≤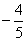 D.x ≥
D.x ≥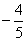
13.一元一次不等式组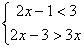 的解集是 ( )
的解集是 ( )
A.-2<x<3 B.-3<x<2 C.x<-3 D.x<2
14.如图1,在数轴上所表示的是哪一个不等式的解集( )
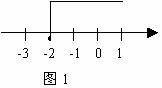
A.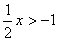 B.
B.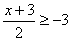 C.x+1≥-1 D.-2x>4
C.x+1≥-1 D.-2x>4
15.如果两个不等式的解集相同,那么这两个不等式叫做同解不等式。下列两个不等式是同解不等式的是 )
A.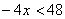 与
与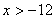 B.
B.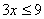 与
与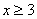
C.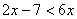 与
与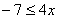 D.
D.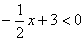 与
与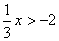
16.解下列不等式组,结果正确的是( )
A.不等式组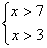 的解集是x>3 B.不等式组
的解集是x>3 B.不等式组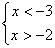 的解集是-3<x<-2
的解集是-3<x<-2
C.不等式组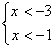 的解集是x<-1 D.不等式组
的解集是x<-1 D.不等式组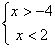 的解集是-4<x<2
的解集是-4<x<2
17.若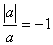 ,则a只能是( )
,则a只能是( )
A.a≤-1 B.a<0 C.a≥-1 D.a≤0
18.关于x的方程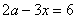 的解是非负数,那么a满足的条件是( )
的解是非负数,那么a满足的条件是( )
A.a>3 B.a≤3 C.a<3 D.a≥3
三、解一元一次不等式(或不等式组),并把它们的解集在数轴上表示出来。
19.6x<7x-2 20.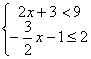
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |