轴对称常见考点例析
河北省唐县北店头中学 马玉涛
轴对称是两个图形之间的一种和谐关系,轴对称图形是一种典雅、优美的图形,两者均深受人们的喜爱,在中考中同样备受命题者的青睐,现将常见的考点作一简单的归纳,希望大家能有所收获。
考点一:考查轴对称图形的识别
下列四个图形中,不是轴对称图形的是

A. B. C. D.
解析:轴对称图形是一种沿某条直线对折后直线两旁的部分能够互相重合的图形,观察图形易知应选D。
评注:判断一个图形是否是轴对称图形的关键是根据定义来确定。
考点二:考查轴对称的性质
例1:如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则
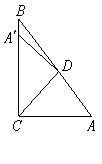
A.40° B.30° C.20° D.10°
解析:因为△ACD沿CD折叠,点A落在点A′处,所以点A与点A′关于CD对称,根据轴对称的性质,
可知∠C A′D=∠A=50°,又△ABC为直角三角形,所以∠B=90°-∠A=40°,又因为∠C A′D是△B A′D的一个外角,所以
评注:图形折叠过程中,折叠前后的两个图形对应线段的长度和对应角的度数保持不变。
例2:已知:如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
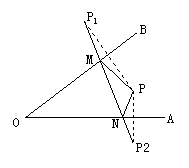
解析:∵点P、
∴PM=
∴△PMN的周长=PM+PN+MN=
评注:本题的思路主要是将线段转化代换,把三角形周长转代为已知线段的和,这种转化的思想是解决数学问题的重要思想方法.
考点三:考查剪纸中的轴对称
如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个( )
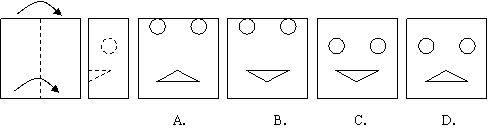
解析:将纸片折叠并进行裁剪,判断展开后图形的形状是一种轴对称变换,由于具有可操作性,考查了学生的动手能力,所以本题可通过折纸的实际操作获得答案为C
评注:动手折叠纸片时一定要注意题目中所给的折叠方向。
考点四:利用轴对称设计图案
例1:图①、图②均为
在图中确定格点
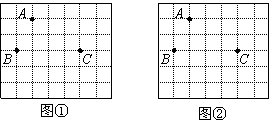

解析:这是一道开放探究型试题,解答时应先确定其对称轴。选择不同的对称轴,会设计出不同的轴对称图形。下面给出两种不同的答案供参考:

评注:对于没有给定对称轴而设计轴对称图案的问题,解题的关键是确定对称轴。
例2:用若干根火柴棒可以摆出一些优美的图案,下图是用火柴棒摆出的一个图案,此图案表示的含义可以是:天平(或公正).请你用5根或5根以上火柴棒摆成一个轴对称图案,并说明你画出的图案的含义.
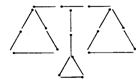
图案:
含义:
解析:这是一道创新型的图案设计题,它不仅考查同学们的想象能力,同时考查了同学们的图案设计能力。答案不唯一,只要有道理就行。
评注:此类问题已成为中考的一大热点。
考点五:轴对称的实际应用(镜面对称):
例1:如图,镜子中号码的实际号码是___________.

解析:镜子中看到的读数与实际的读数关于镜子成轴对称,因此,欲知实际读数,最简单的办法是从考卷的背面观看,或拿面镜子观看;如果这两种办法无法实施,那就只好采用倒读,并注意每个数字的轴对称性.如5的轴对称变成了2,2的轴对称变成了5,因此,实际号码是3265.
评注:实际物体与镜子里的像关于镜面成轴对称。
例2:一面镜子MN竖直悬挂在墙壁上,人眼O的位置.如图所示,有三个物体A、B、C放在镜子前面,人眼能从镜子看见哪个物体?
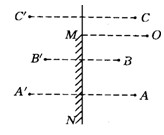
解析:物体在镜子里面所成的像就是数学问题中的物体关于镜面的对称点,人眼从镜子里所能看见的物体,它关于镜面的对称点,必须在眼的视线范围内.所以分别作A、B、C三点关于直线MN的对称点A′、B′、C′.显然人能从镜子里只能看见A、B两物体.
评注:这道题是轴对称在实际中的应用,关键是建立相应的轴对称图形的数学模型,再利用轴对称知识来解决.
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |