2.2转化思想
代表性题型:面积问题,二函数图象与坐标轴的交点距离、二次函数与一次函数交点距离、反比例函数与一次函数交点距离问题(与一元二次方程根的系数关系转化)。
例2.已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1)。
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式。(4分)
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E。
①当△BDE是等腰三角形时,直接写出此时点E的坐标。(3分)
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由。(3分)
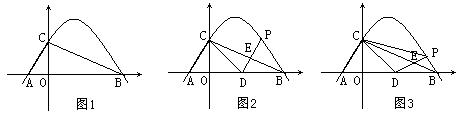
解析:⑴由Rt△AOC∽Rt△COB易知,CO2=OA.OB=OA(AB-OA),可求OA=1,OB=4
∴A(-1,0) B(4,0) C(0,2) 可设解析式为y=a(x+1)(x-4),
将点C(0,2)代入,可求a=![]() ∴
∴![]() 为所求
为所求
⑵![]() ;
;![]()
![]()
提示:①ED=EB时,过E作BD垂线,可得![]()
②直线BC的解析式为![]() ,设
,设![]() ,利用勾股定理和点
,利用勾股定理和点![]() 在直线BC上,可得两个方程组
在直线BC上,可得两个方程组
 分别可求
分别可求![]() 和
和![]() 。
。
⑶方法1:连OP。如图4。

P(m,n)在抛物线![]() 上
上
∴P(m, ![]() )
)
S△CPO=S四边形ODPC-S△OCD
=S△POC+ S△PDO-S△OCD=![]() OC·|xp|+
OC·|xp|+![]() OD·|yp|—
OD·|yp|—![]() OC·OD
OC·OD
=![]() ×2m+
×2m+![]() ×2(
×2(![]() )-
)-![]() ×2×2
×2×2
=-![]() m
m![]() +
+![]() m=-
m=-![]() (m-
(m-![]() )
)![]() +
+![]()
当m=![]() 时,S△CPO面积最大,此时P(
时,S△CPO面积最大,此时P(![]() ,
,![]() )
)
方法2:过D作X轴的垂线,交PC于M,如图5。
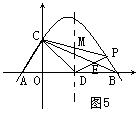
易求PC的解析式为![]() ,且
,且![]() ,故
,故
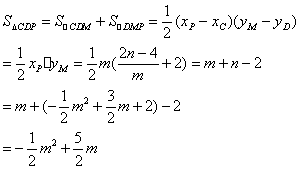
∴当![]() 时,
时,![]() ,
,![]()
思想方法解读:本题是一道二次函数与平面几何综合的压轴题
第⑴问由三角形形似(或射影定理)求出相关线段的长,写出相应点的坐标。然后灵活设置二次函数式,用待定系数法求出二次函数式。
第⑵问,虽然题目要求是直接写出点E的坐标。但点E的坐标必须通过计算得到。而在计算的过程中,要考虑符合要求的等腰三角形的多样性,需分类讨论顶点、腰的对应情况。
第⑶问是本题的难点。题中的面积表示,要结合P(m,n)在抛物线上,充分利用点的坐标的几何意义,或是利用平面几何的性质,有效表示△BCD的面积,将不能直接表示的三角形面积转化为能用已知线段和P点坐标表示的面积。方法1是将四边形分割成两个三角形△POC、△POD,方法2,是通过过D点作垂线,直接将△BDC转化为△PDM、△CDM。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |