2.3极端值思想
代表性题型:动态几何问题,动态函数问题。
例3.已知![]() 为线段
为线段![]() 上的动点,点
上的动点,点![]() 在射线
在射线![]() 上,且满足
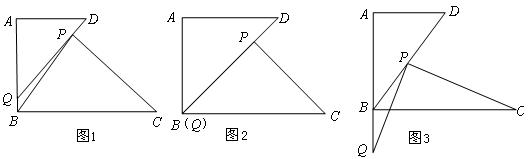
上,且满足![]() (如图1所示).
(如图1所示).
(1)当![]() ,且点
,且点![]() 与点
与点![]() 重合时(如图2所示),求线段
重合时(如图2所示),求线段![]() 的长;
的长;
(2)在图1中,联结![]() .当
.当![]() ,且点
,且点![]() 在线段
在线段![]() 上时,设点
上时,设点![]() 之间的距离为
之间的距离为![]() ,
,![]() ,其中
,其中![]() 表示
表示![]() 的面积,
的面积,![]() 表示
表示![]() 的面积,求
的面积,求![]() 关于
关于![]() 的函数解析式,并写出函数定义域;
的函数解析式,并写出函数定义域;
(3)当![]() ,且点
,且点![]() 在线段
在线段![]() 的延长线上时(如图3所示),求
的延长线上时(如图3所示),求![]() 的大小。
的大小。
解析:(1)AD=2,且Q点与B点重合。由![]() =1,∴PB(Q)=PC,△PQC为等腰直角三角形,BC=3,PC=Bccos45°=3×
=1,∴PB(Q)=PC,△PQC为等腰直角三角形,BC=3,PC=Bccos45°=3×![]() =
=![]() 。
。
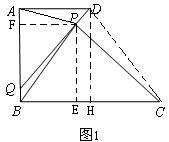
(2)如图:作PE⊥BC,PF⊥AQ。BQ=x,则AQ=2-x。
由△BPF∽△BDP,![]() =
=![]() =
=![]() ,又BF=PE
,又BF=PE
∴![]() =
=![]() ,∴PF=
,∴PF=![]() PE
PE
S△APQ=![]() (2-x)PF,S△PBC=
(2-x)PF,S△PBC=![]() ×3PE
×3PE
∴y=![]() (2-x)
(2-x)
P点与D点重合时,此时CQ取最大值。过D作DH⊥BC。
CD=![]() ,此时
,此时![]() =
=![]() ,
,![]() =
=![]() ,PQ=
,PQ=![]() ,BQ=AB-AQ=
,BQ=AB-AQ=![]()
∴函数的定义域:0≤x≤![]()
(3)方法1:PQ/PC=AD/AB,假设PQ不垂直PC,则可以作一条直线PQ′垂直于PC,与AB交于Q′点,则:B,Q′,P,C四点共圆。
由圆周角定理,以及相似三角形的性质得:PQ′/PC=AD/AB,
又由于PQ/PC=AD/AB 所以,点Q′与点Q重合,所以角∠QPC=90°
方法2:如图3,作PM⊥BC,PN⊥AB。由![]() =
=![]() =
=![]() ,即
,即![]() ==
==![]()
∴△PNQ∽△PMC ∠MPC=∠NPN,∴∠QPC=∠MPC+∠QPB=∠NPQ+∠QPM=90°
思想方法解读:这是一道动态几何的变式综合题。
第⑴问,线段的比值![]() 不变,Q在特殊点(与B点重合),由AD=AB=2,故PQ(B)=PC,△PQC为等腰直角三角形。利用几何性质可求出PC。
不变,Q在特殊点(与B点重合),由AD=AB=2,故PQ(B)=PC,△PQC为等腰直角三角形。利用几何性质可求出PC。
第⑵问中利用三角形相似比,结合已知条件中的固定线段比,找出△PAQ、△PBC高之间的比例关系,是求函数式的关键。而第二问中写出函数的定义域则是难点。需分析出P点运动的极端情况,当P与D重合时,BQ取得最大值。集合图形的几何性质及已知条件中的固定线段比,求出此时BQ的长度,既为BQ的最大值。体现极端值思想。
⑶中可以用四点共圆通过归一法求证,也可以通过构造相似形求证。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |