转化思想求解问题两例
甘肃省镇原县王寨初中 慕志明
例1 已知
，求
的值．
解：由可得：
，
=4z;
,y=
=6z. x+3y-z=4z+18z-z=21z,2x-y+z=8z-6z+z=3z
=
=7.
例2 如图1所示，ΔABC是等边三角形，P为三角形内任一点，PD//AB交BC于D，PE//BC交AC于E，PF//CA交AB于F，若三角形的周长为18cm，试求PE+PD+PF的值．
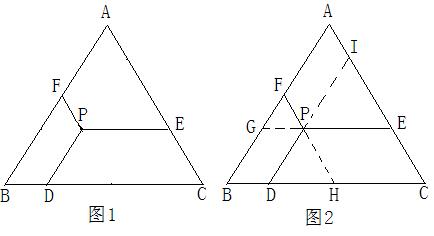
解：延长EP交AB于G，延长FP交BC于H，延长DP交AC于I(如图２所示)，则：
∵GE//BC
∴∠FGP=∠ABC=60
,∠GEA=∠BCA=60(两直线平行，同位角相等)
∵FH//AC
∴∠GFP=∠BAC=60,∠GPF=∠GEA=60
(两直线平行，同位角相等) ∴∠FGP=60，∠GFP=60，∠GPF=60（等量代换）
∴ΔFPG是等边三角形（三个角都是60的三角形为等边三角形）
∴FP=FG（等边三角形的任意两条边相等）
∵GE//BC
∴∠PEI∠BCA=60,∠AGE=∠ABC=60(两直线平行，同位角相等)
∵GI//BA
∴∠PIE=∠BAC=60,∠IPE=∠AGE=60(两直线平行，同位角相等)
∴∠PIE=60，∠IPE=60，∠PEI=60（等量代换）
∴ΔIPE是等边三角形（三个角都是60的三角形为等边三角形）
∴PE=PI（等边三角形的任意两条边相等）
又∵
PI//FA，FP//IA∴四边形AIPF是平行四边形（两组对边分别平行的四边形为平行四边形）
∴PI=FA（平行四边形的对边相等）
∴PE=FA（等量代换）
又∵PD//GB,PD//GB
∴四边形PDGB是平行四边形（两组对边分别平行的四边形为平行四边形）
∴PD=GB（平行四边形的对边相等）
∴PE+PF+PD=AF+FG+GB=AB=
(AB+BC+CA)= 
18cm=6cm
即：PE+PD+PF＝6cm．
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |