用对顶三角形的性质求角
湖北省黄石市下陆中学 周国强
线段AB 、CD相交于点O，连结AB、CD，我们把这样的基本图形称之为“对顶三角形”（如图所示）．显见，“对顶三角形形”有如下性质：∠A+∠D＝∠C+∠B（读者可自已证明）．
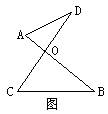
对于求角问题，若图形中含有“8字形”， 运用“8字形”的性质求解，可获事半功倍之效．
例1 如图1，∠A+∠B+∠C+∠D+∠E＋∠F＝_____度．
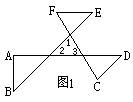
析解：图中有若干个现成的“8字形”．因为∠A+∠B＝∠1＋∠3 ，∠C+∠D＝∠1＋∠2，∠E＋∠F＝∠2＋∠3，
所以∠A+∠B+∠C+∠D+∠E＋∠F＝2（∠1＋∠2＋∠3）＝2×180
＝360．
例2 如图2，在五角星中，求∠A+∠B+∠C+∠D+∠E的度数。
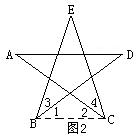
析解：图中虽有现成的“8字形”，但不易将这五个角集中到同一三角形中来，故连BC，构造新的“8字形”．因为∠1+∠2＝∠A＋∠D，所以∠A+∠B+∠C+∠D+∠E＝∠1＋∠2＋∠3＋∠4＋∠E＝∠E＋∠EBC＋∠ECB＝180．
例3如图3，若∠A＝120，∠B＝45， ∠E＝33
，∠F＝108求∠COD的度数． 
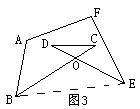
析解：连BE，构造四边形ABEF，因为∠A+∠ABE+∠BEF＋∠F＝360，所以∠C+∠D＝∠CBE+∠DEB＝360－（120
＋45＋33＋108）＝54，从而∠COD=126． 例4如图4，已知 ∠E＋∠F＝∠H，求：∠A＋∠B＋∠ACD＋∠CDG的度数．
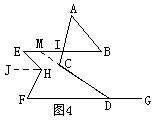
析解：过点H作HJ∥EB，则∠E＝∠EHJ，因为∠E＋∠F＝∠H，所以∠JHF＝∠F，所以HJ∥FG，从而EB∥FG．延长DC交EB于M，则∠BMD＋∠MDG＝180，又∠ICM＋∠ICD＝180，所以∠A＋∠B＋∠ACD＋∠CDG＝∠ICM＋∠IMC＋∠ACD＋∠CDG＝（∠ICM＋∠ACD）＋（∠IMC＋∠CDG）＝180＋180
＝360． 例5 如图5，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．解答下列问题：
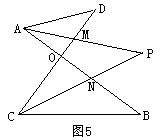
(1)若∠D＝40，∠B＝36，求∠P的度数；
(2)如果图中的∠D和∠B为任意角时，其它条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系？（直接写出结论即可）
析解：
（1）由“8字形”的性质知∠DAP＋∠D＝∠DCP＋∠P，
∠PCB＋∠B＝∠PAB＋∠P，
即∠P＝∠DAP＋∠D－∠DCP ①，
∠P＝∠PCB＋∠B－∠PAB ②．
由条件知∠DAP＝∠PAB，∠PCB＝∠DCP，
①＋②得 2∠P＝∠D＋∠B＝40＋36＝76，
（2）仿（1）易知∠P与∠D、∠B之间的之间的关系为∠P＝
（∠D＋∠B）．
练习：
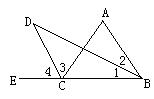
如图，BD是△ABC中∠ABC的角平分线，CD是△ABC的外角∠ACE的平分线，它与BD的延长线交于点D，我们将会得到∠A＝2∠D这一结论，试想一想为什么？并加以说明．
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |