不尽的探索 无穷的乐趣
湖北省襄阳市襄州区黄集镇初级中学 赵国瑞
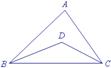
引例 如图1,在△ABC中,∠ABC、∠ACB的平分线相交于点O,试判断∠BOC与∠A的关系?说明你的理由.
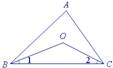
图1
解:∠BOC=90°+
理由:∵BO平分∠ABC,CO平分∠ACB,
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠
∠
∴∠1+∠2=![]() (∠ABC+∠ACB).
(∠ABC+∠ACB).
在△ABC中,∠ABC+∠ACB=180°-∠A.
∴∠1+∠2=![]() (180°-∠A)=90
(180°-∠A)=90
在△BOC中,∠BOC=180°-(∠1+∠2)
=180°-(90°-![]() ∠A)=90
∠A)=90
由此我们得到这样一个结论:
结论1:三角形两内角平分线的夹角等于第三个内角的一半的余角的补角.
如果把题目中的内角平分线,改为外角的平分线,那么∠BOC与∠A的关系又如何呢?
探索一:如图2,△
ABC的外角∠CBM、∠BCN的平分线相交于点O,试判断∠BOC与∠A的关系?说明你的理由.
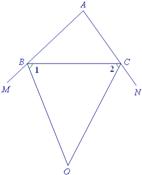
图2
解:∠BOC=90°-![]() ∠
∠
理由:∵BO平分∠CBM,CO平分∠BCN,
∴∠1=![]() ∠CBM,∠2=
∠CBM,∠2=![]() ∠BCN.
∠BCN.
∴∠1+∠2=![]() (∠
(∠
∵∠CBM=180°-∠ABC,∠BCN=180°-∠ACB,
∴∠CBM +∠BCN=360°-(∠ABC+∠ACB)
=360°-(180°-∠A)=180°+∠A.
∴∠1+∠2=![]() (180
(180
在△BOC中,∠BOC=180°-(∠1+∠2)
=180°-(90°+![]() ∠A)=90°-
∠A)=90°-
说明:在计算∠CBM +∠BCN时,也可利用三角形的外角性质,即∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,所以∠CBM +∠BCN=(∠A+∠ACB+∠ABC)+∠A=180°+∠A.
为了利用结论1,本题也可以这样说明理由:
如图3,分别作∠ABC和∠ACB的平分线BP和
CP,BP和CP相交于点P,根据“一对邻补角的平分线互相垂直”(此结论留给同学们自己探索),可得∠PBO=90°,∠PCO=90°.又四边形PBOC的内角和等于360°,所以∠BOC=360°-90°-90°-∠BPC=180°-∠BPC.
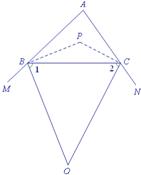
图3
利用结论1,可得∠BPC=90°+![]() ∠A.
∠A.
所以∠BOC=180°-(90°+![]() ∠
∠
由此我们得到这样一个结论:
结论2:三角形两外角平分线的夹角等于与这两外角不相邻的内角的一半的余角.
以上分别是两内角平分线与两外角平分线相交的情况,如果是一内角的平分线与一外角的平分线相交,结果又会如何呢?
探索二:如图4,在△
ABC中,内角∠ABC的平分线与外角∠ACD的平分线相交于点O,试说明∠BOC与∠A的关系?说明你的理由.
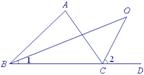
图4
解:∠BOC=![]() ∠
∠
理由:∵BO平分∠ABC,CO平分∠ACD,
∴∠ABC=2∠1,∠ACD=2∠2.
又∠2是△BOC的外角,
∴∠2=∠1+∠BOC,即∠BOC=∠2-∠1.
又∠ACD是△ABC的外角,
∴∠ACD=∠ABC +∠A,即∠A=∠ACD -∠ABC.
∴∠A=2∠2-2∠1=2(∠2-∠1)=2∠BOC.
∴∠BOC=![]() ∠A.
∠A.
为了利用结论1,本题也可以这样说明理由:
如图5,作∠ACB的平分线CP交BO于点P,利用结论1可知∠BPC=90°+![]() ∠
∠
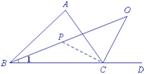
图5
为了利用结论2,本题也可以作△ABC的外角平分线与CO的反向延长线相交于点P(如图6),易证CP是△ABC的外角∠BCE的平分线,根据“一对邻补角的平分线互相垂直”可知∠PBO=90°.又由结论
2可知∠BPC=90°-
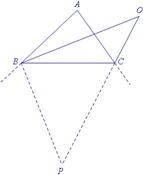
图6
同学们,阅读此文,你是否有一种沉浸在不尽的探索和喜悦之中,在探索的过程中,我们又利用探索出来的结论(或者叫做我们的小发明或小创造吧)去探索新的结论,你是否有一种小小的成就感呢?
有人算过这样一笔帐,一只蜜蜂要酿出一公斤蜂蜜,需要来回飞行大约三十万公里,吸吮大约一千二百万个花朵的液汁.每次采集回来,还需要把液汁从胃里吐出来,由另一只蜜蜂吸到自己的胃里,如此吞吞吐吐一百二十次到三百四十以次,液汁才成为蜜汁,并最终变成浓稠的蜂蜜.
由此可见积累的重要性,学习数学也需要积累.数学解题能力的提高,需要积累丰富的解题经验,并适当记住一些简洁的结论,可以快速抓住问题的本质,简化思维过程,提高解题效率.
快乐体验:
1.如图7,BD平分∠ABC,CD平分外角∠ACE,∠A=70°,求∠D的度数.
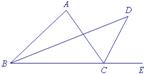
图7
2.如图8,BD平分∠ABC,CD平分∠ACB,∠A=70°,求∠D的度数.
3.如图9,BD平分∠CBE,CD平分∠BCF,∠A=70°,求∠D的度数.
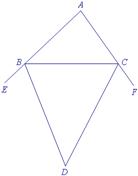
图9
4.如图10,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=___.(提示:先证AP是△ABC的外角平分线)
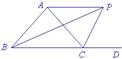
图10
参考答案:1.35°;2.125°;3.55°;4.50°
引例 如图1,在△ABC中,∠ABC、∠ACB的平分线相交于点O,试判断∠BOC与∠A的关系?说明你的理由.

图1
解:∠BOC=90°+![]() ∠A.
∠A.
理由:∵BO平分∠ABC,CO平分∠ACB,
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=
在△ABC中,∠ABC+∠ACB=180°-∠A.
∴∠1+∠2=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
在△BOC中,∠
BOC=180°-(∠1+∠2)
=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A.
∠A.
由此我们得到这样一个结论:
结论1:三角形两内角平分线的夹角等于第三个内角的一半的余角的补角.
如果把题目中的内角平分线,改为外角的平分线,那么∠BOC与∠A的关系又如何呢?
探索一:如图2,△ABC的外角∠CBM、∠BCN的平分线相交于点O,试判断∠BOC与∠A的关系?说明你的理由.

图2
解:∠BOC=90°-![]() ∠A.
∠A.
理由:∵BO平分∠CBM,CO平分∠BCN,
∴∠1=![]() ∠CBM,∠2=
∠CBM,∠2=![]() ∠BCN.
∠BCN.
∴∠1+∠2=
∵∠CBM=180°-∠ABC,∠BCN=180°-∠ACB,
∴∠CBM +∠BCN=360°-(∠ABC+∠ACB)
=360°-(180°-∠A)=180°+∠A.
∴∠1+∠2=![]() (180°+∠A)=90°+
(180°+∠A)=90°+![]() ∠A.
∠A.
在△BOC中,∠BOC=180°-(∠1+∠2)
=180°-(90°+![]() ∠
∠
说明:在计算∠CBM +∠BCN时,也可利用三角形的外角性质,即∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,所以∠CBM +∠BCN=(∠A+∠ACB+∠ABC)+∠A=180°+∠A.
为了利用结论1,本题也可以这样说明理由:
如图3,分别作∠
ABC和∠ACB的平分线BP和CP,BP和CP相交于点P,根据“一对邻补角的平分线互相垂直”(此结论留给同学们自己探索),可得∠PBO=90°,∠PCO=90°.又四边形PBOC的内角和等于360°,所以∠BOC=360°-90°-90°-∠BPC=180°-∠BPC.

图3
利用结论1,可得∠BPC=90°+![]() ∠A.
∠A.
所以∠BOC=180°-(90°+![]() ∠
∠
由此我们得到这样一个结论:
结论2:三角形两外角平分线的夹角等于与这两外角不相邻的内角的一半的余角.
以上分别是两内角平分线与两外角平分线相交的情况,如果是一内角的平分线与一外角的平分线相交,结果又会如何呢?
探索二:如图4,在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线相交于点
O,试说明∠BOC与∠A的关系?说明你的理由.

图4
解:∠BOC=![]() ∠A.
∠A.
理由:∵BO平分∠ABC,CO平分∠ACD,
∴∠ABC=2∠1,∠ACD=2∠2.
又∠2是△BOC的外角,
∴∠2=∠1+∠BOC,即∠BOC=∠2-∠1.
又∠ACD是△ABC的外角,
∴∠ACD=∠ABC +∠A,即∠A=∠ACD -∠ABC.
∴∠A=2∠2-2∠1=2(∠2-∠1)=2∠BOC.
∴∠BOC=![]() ∠
∠
为了利用结论1,本题也可以这样说明理由:
如图5,作∠ACB的平分线CP交BO于点P,利用结论1可知∠BPC=90°+![]() ∠A.根据“一对邻补角的平分线互相垂直”可知∠PCO=90°.又∠BPC是△PCO的外角,所以∠BPC=∠BOC+∠BPC,即90°+
∠A.根据“一对邻补角的平分线互相垂直”可知∠PCO=90°.又∠BPC是△PCO的外角,所以∠BPC=∠BOC+∠BPC,即90°+![]() ∠
∠

图5
为了利用结论2,本题也可以作△ABC的外角平分线与CO的反向延长线相交于点P(如图6),易证CP是△ABC的外角∠BCE的平分线,根据“一对邻补角的平分线互相垂直”可知∠
PBO=90°.又由结论2可知∠BPC=90°-

图6
同学们,阅读此文,你是否有一种沉浸在不尽的探索和喜悦之中,在探索的过程中,我们又利用探索出来的结论(或者叫做我们的小发明或小创造吧)去探索新的结论,你是否有一种小小的成就感呢?
有人算过这样一笔帐,一只蜜蜂要酿出一公斤蜂蜜,需要来回
飞行大约三十万公里,吸吮大约一千二百万个花朵的液汁.每次采集回来,还需要把液汁从胃里吐出来,由另一只蜜蜂吸到自己的胃里,如此吞吞吐吐一百二十次到三百四十以次,液汁才成为蜜汁,并最终变成浓稠的蜂蜜.
由此可见积累的重要性,学习数学也需要积累.数学解题能力的提高,需要积累丰富的解题经验,并适当记住一些简洁的结论,可以快速抓住问题的本质,简化思维过程,提高解题效率.
快乐体验:
1.如图7,BD平分∠ABC,CD平分外角∠ACE,∠A=70°,求∠D的度数.

图7
2
.如图8,BD平分∠ABC,CD平分∠ACB,∠A=70°,求∠D的度数.

图8
3.如图9,BD平分∠CBE,CD平分∠BCF,∠A=70°,求∠D的度数.

图9
4.如图10,△ABC的外角∠
ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=___.(提示:先证AP是△ABC的外角平分线)

图10
参考答案:1.35°;2.125°;3.55°;4.50°
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |