2012中考数学热点知识归纳 91

这道中考题的解法真多

湖北省襄阳市襄州区黄集镇初级中学　赵国瑞

2010年湖北省武汉市中考题第24题：

已知：线段OA⊥OB，点C为OB中点，D为线段OA上一点．连结AC，BD交于点P．

(1)如图1，当OA=OB，且D为OA中点时，求的值；

(2)如图2，当OA=OB，且时，求tan∠BPC的值．

(3)如图3，当AD∶AO∶OB=1∶n∶时，直接写出tan∠BPC的值．

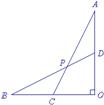
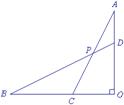
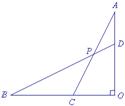
　图1 　　　　　图2 　　　　图3

分析：(1)要求的值，联想到平行线分线段成比例定理

或平行于三角形一边的直线和其他两边(或两边的延长线)，所构成的三角形与原三角形相似(当然，由于已知条件中有中点这个条件，还可以联想到三角形中位线定理，或者三角形的面积)，因此应设法构造平行线．

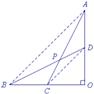
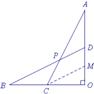
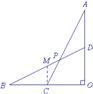
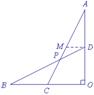
　　　　　　图4 　　　图5 　　　图6 　　图7

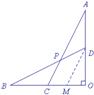
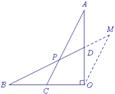
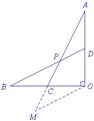
　　　　　　图8　　　　　　　　图9 　　　　　　　　图10

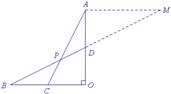
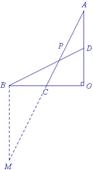
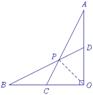
　　图11 　　　　　　图12 　　　　　　　　　图13

思路一：构造中位线

解法1：连结AB、CD，如图4，则CD是△AOB的中位线．

∴CD∥AB，且CD=AB．∴△CPD∽△APB．

∴=

=2．

思路二：构造平行线

解法2：过点C作CM∥BD交AO于M，如图5．

∵C为OB中点，由平行线分线段成比例定理，得DM=MO，=．

∵D为OA中点，且DM=MO，∴AD=2DM，即==2．

解法3：过点C作CM∥AO交BD于M，如图6．

解法4：过点D作DM∥BO交AC于M，如图7．

解法5：过点D作DM∥AC交BO于M，如图8．

解法6：过点O作OM∥BD交AC的延长线于M，如图9．

解法7：过点O作OM∥AC交BD的延长线于M，如图10．

解法8：过点A作AM∥BO交BD的延长线于M，如图11．

解法9：过点B作BM∥AO交AC的延长线于M，如图12．

(解法3至解法9的过程留给同学们自己完成)

思路三：利用面积

解法10：连结OP，如图13．

∵点C为OB中点，D为OA中点，∴S_△BCP=S_△OCP，S_△ADP=S_△ODP．

∵OA=OB，OA⊥OB，∴S_△AOC=S_△BOD．

∴S_△AOC-S_{四边形ODPC}=S_△BOD-

S_{四边形ODPC}，即S_△BCP=S_△ADP．

∴S_△BCP=S_△OCP=S_△ADP=S_△ODP．

∴==2．

(2)

要求tan∠BPC的值，注意到∠BPC及其对顶角所在的三角形不是直角三角形，且在两个直角三角形中也无法找到与∠BPC相等的角，因此需要以∠BPC为内角构造直角三角形．另外，为了找出所构造的直角三角形中两直角边的关系，仍然需要作出问题(1)中的辅助线．

解法1

：过点C作CE⊥BD于E，过点D作DM∥BO交AC于M，如图14，则．

设AD=k(k＞0)，则AO=4k=OB，DO=AO-AD=4k-k=3k．

∵C为OB中点，∴BC=CO=2k．

在Rt△BOD中，由勾股定理，得BD===5

k．

∵DM∥BO，∴．∴BP=4k．

易证△BEC∽△BOD，∴，即．

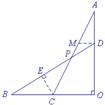
　　　　　　　　　　　　　　　　　　图14

∴CE=1.2k，BE=1.6k．∴EP=BP-BE=4k-1.6k=2.4k．

∴tan∠BPC=．

事实上，过点C作CE⊥BD于E后，再作一条与图5～图12中的任何一个图形一样的辅助线，都可以得到一种解法，这样我们就可以得到8种解法．而且在解题过程中，我们又发现了一种比较简捷的方法．

如解法1中，由BD=5k，，得PD=k．而AD=k，于是PD=AD，∠BPC=∠APD=∠A．从而tan∠BPC=tanA=．这是我们在按照常规方法解题的过程中，由于发现线段的相等关系而得到的简捷求法，这是意外的收获．

因此我们也可以只作一条辅助线，辅助线的作法同图5～图12中的任何一个图形的辅助线作法一样，于是我们又得到问题(2)的8种求法．

(3)当AD∶AO∶OB=1∶n∶时，在tan∠

BPC的值时，我们仍然可以像解决问题(2)那样，通过作辅助线求出tan∠BPC的值，但由于已知线段间的数量关系以字母比值的形式给出，这给问题的求解带来极大的不便，而且题目要求直接写出tan∠BPC的值，问题(2)也已经求出了tan∠BPC的值，因此我们应该设法将问题(3)与问题(2)联系在一起．问题(2)中的tan∠BPC值是在“OA=OB，且”这个条件下得到的，要想求出当AD∶AO∶OB=1∶n∶时tan∠BPC的值，就要设法将条件“OA=OB，且”与与“OA=OB，且”发生联系．通过观察不难发现，当n=4时，=4，此时AD∶AO∶OB=1∶4∶4，正好满足“OA=OB，且”，因此当n=4时，必然有tan∠BPC=．而tan∠BPC==，且当n=4时，=2，因此我们有理由猜测：当AD∶AO∶OB=1∶n∶时，tan∠BPC=．

评注：本题是一道考查平行线分线段成比例、三角形相似、勾股定理及三角函数的综合题，由三个小题组成，这三个小题的难度呈梯度上升，是一道典型的“递进型”中考题．

其中问题(1)中的解法1是根据已知条件中有两个中点，从而想到三角形的中位线定理而作的辅助线，是问题(1)的最简捷解法．解法10也是根据中点想到的辅助线作法．而解法2至解法9是为了利用平行线分线段成比例或构造相似三角形而作的辅助线，其中图5、图6、图7和图8(所作的辅助线没有与已知线段的延长线相交)解答问题(1)常见的辅助线作法．

在解答问题(2)时，因为∠BPC及其对顶角所在的三角形都是非直角三角形，而且从已知条件中我们无法再找出与∠BPC相等的角，为了求出tan∠BPC的值，我们应该首当其充地构造∠BPC所在的直角三角形，于是过点C作CE⊥BD于E，至于过其它点作另一条辅助线，一是为了求出线段PD、BP的比值，从而顺利找出所构造的直角三角形中两直角边的关系，另外这也是由“递进型”中考题的特点(下一题要充分用到上一题的结论或解题思路)决定的．在求解过程中，我们发现PD=AD，于是∠BPC=∠APD=∠A，而∠A在直角三角形中，且正切值容易求出，于是把求tan∠