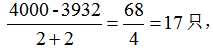在考场上人与人拉开差距的除了平常的知识点的积累,还有面对考试题型能够有一个更好的解答思路,下面由出国留学网小编为你精心准备了“行测数量关系:鸡兔同笼”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系:鸡兔同笼
行测数量运算部分一直是考生认为难度最大的一个板块,通常10道数学运算题目,准确率往往难以达到50%,甚至是花费了大量的时间来做该部分。那么原因主要还是学员对这部分题目有着畏怯的心理,未战先败;另外的原因就是在做这一部分题目的时候缺乏相应的方法和技巧,导致浪费了大量的时间在一些所谓的难题上。
今天跟大家分享盈亏思想中的一个模型——鸡兔同笼,能够解决一类问题,较列方程会比较方便。
一、经典例题
大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中各有几只鸡和兔?
1.方程法:
解:设鸡、兔各有x, y.
根据等量关系可以得到x+y=35;2x+4y=94.
这样可以得到x=23, y=12
2.盈亏思想(鸡兔同笼):
解:可将笼中动物全部看成鸡(兔亦可),这样35只鸡有35个头和70只脚,会发现脚的数量还差24只。之所以脚的数量对不上,是因为其中的一些兔子被当成了鸡,一只兔子看成一只鸡,就少掉2只脚,所以一共少了24只脚,就对应把12只兔子看成了12只鸡。因此就得到了兔子的数量为12,所以鸡的数量就为23.
3.解法特征
如果先设的是鸡,求出来的是兔子;如果先设的是兔子,则求出来的鸡。
4.题型特征
存在两个总量(一共35个头,一共94只脚);存在两个分量(一只鸡有2只脚,一只兔子有4只脚)
二、应用
某餐厅设有可坐12人和可坐10人两种规格的餐桌共18张,最多可容纳208人同时就餐,问该餐厅有几张10人桌?
A.2 B.4 C.6 D.8
【答案】B。解析:题干中出现了以下的题型特征,两个总量(一共18张桌子,一共可坐208人),两个分量(一桌可坐12人,一桌可坐10人),所以我们可以直接利用鸡兔同笼模型解答。设全为12人桌,则共12*18=216人,实际上只有208人,所以(216-208)/(12-10)=4为所求,故选B。
推荐阅读: