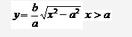
高中数学选修1-1《双曲线》教案【一】
教学准备
教学目标
教学目标: 1.能用与椭圆对比的方法分析并掌握双曲线的范围、对称性、顶点等几何性质;
2.掌握双曲线的渐近线的概念和证明;
3.明确双曲线标准方程中a、b、c的几何意义;
4.能根据双曲线的几何性质确定双曲线的方程, 并解决简单问题.
教学重难点
教学重点: 双曲线的几何性质
教学难点: 双曲线的渐近线
教学过程
教学过程:
一、知识回顾:
1. 双曲线的标准方程;
2. 椭圆的几何性质及其研究方法.
二、课堂新授:
1. 要求学生按照研究椭圆几何性质的方法, 研究双曲线
的几何性质.
(1) 范 围: 双曲线在不等式x≤-a与x≥a所表示的区域内.
(2) 对称性: 双曲线关于每个坐标轴和原点都是对称的. 这时, 坐标轴是双曲线的对称轴, 原点是双曲线的对称中心. 双曲线的对称中心叫做双曲线的中心.
(3) 顶 点: 双曲线和它的对称轴有两个交点, 它们叫做双曲线的顶点.
顶点坐标A1 (-a, 0), A2 (a, 0)
① 线段A1A2叫做双曲线的实轴, 它的长等于2a, a叫做双曲线的实半轴长.
② 双曲线与y轴没有交点, 取点B1 (0,-b)、 B2 (0, b), 线段B1B2叫做双曲线的虚轴, 它的长等于2b, b叫做双曲线的虚半轴长.
(4) 离心率: 双曲线的焦距与实轴长的比e = , 叫做双曲线的离心率.
双曲线的离心率的取值范围是 (1, +∞).
2. 双曲线的渐近线
(1) 观察: 经过A2、A1作y轴的平行线x = ±a, 经过B2、B1作x轴的平行线y = ±b, 四条直线围成一个矩形. 矩形的两条对角线所在直线的方程是y =±x, 观察可知: 双曲线的各支向外延伸时, 与这两条直线逐渐接近.
(2) 证明: 取双曲线在第一象限内的部分进行证明. 这一部分的方程可写为
高中数学选修1-1《双曲线》教案【二】
教学准备
教学目标
1、熟练掌握曲线的方程和方程的曲线概念;
2、掌握坐标法和解析几何的概念
3、掌握根据已知条件求平面曲线方程的基本步骤;
4、学会根据已知条件求简单的平面曲线的方程。
5、学会判断曲线和方程的关系。
教学重难点
掌握...