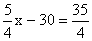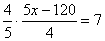一元一次方程作为数学中常见到的题型之一,它的解法步骤有哪些呢。以下是由出国留学网编辑为大家整理的“一元一次方程的解法步骤”,仅供参考,欢迎大家阅读。
一元一次方程的解法步骤
(1)中学数学——配方法的步骤:
先把常数项移到方程的右边,再把二次项的系数化为1,再同时加上1次项的系数的一半的平方,最后配成完全平方公式
(2)中学数学——分解因式法的步骤:
把方程右边化为0,然后看看是否能用提取公因式,公式法(这里指的是分解因式中的公式法)或十字相乘,如果可以,就可以化为乘积的形式
(3)中学数学——公式法
就把一元二次方程的各系数分别代入,这里二次项的系数为a,一次项的系数为b,常数项的系数为c。
拓展阅读:
一元二次方程的解法
大家知道,二次函数有顶点式(-b/2a,4ac-b2/4a),这大家要记住,很重要,因为在上面已经说过了,一元二次方程也是二次函数的一部分,所以他也有自己的一个解法,利用他可以求出所有的一元一次方程的解
(1)中学数学——配方法
利用配方,使方程变为完全平方公式,在用直接开平方法去求出解
(2)中学数学——分解因式法
提取公因式,套用公式法,和十字相乘法。在解一元二次方程的时候也一样,利用这点,把方程化为几个乘积的形式去解
(3)中学数学——公式法
这方法也可以是在解一元二次方程的万能方法了,方程的根X1={-b+√[b2-4ac)]}/2a,X2={-b-√[b2-4ac)]}/2a。
一元二次方程根的情况
利用根的判别式去了解,根的判别式可在书面上可以写为“△”,读作“diao ta”,而△=b2-4ac,这里可以分为3种情况:
I当△>0时,一元二次方程有2个不相等的实数根;
II当△=0时,一元二次方程有2个相同的实数根;
III当△<0时,一元二次方程没有实数根(在这里,学到高中就会知道,这里有2个虚数根)
韦达定理
利用韦达定理去了解,韦达定理就是在一元二次方程中,二根之和=-b/a,二根之积=c/a。
也可以表示为x1+x2=-b/a,x1x2=c/a。利用韦达定理,可以求出一元二次方程中的各系数,在题目中很常用。
...

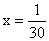
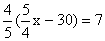 ,下列变形较简便的是( )
,下列变形较简便的是( )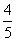 ,得
,得