在考场上人与人拉开差距的除了平常的知识点的积累,还有面对考试题型能够有一个更好的解答思路,下面由出国留学网小编为你精心准备了“行测数量关系技巧:巧妙利用题干解决数学问题”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:巧妙利用题干解决数学问题
数量关系是行测考试中的常考题型,这类题目题量大,题目难,考点多,导致很多考生产生了放弃的想法。但是现在随着就业难,再加疫情影响,有更多的人选择考公务员,公务员考试分数势必会增加,放弃数量关系可能会导致整体分数不高,而与公务员擦肩而过。对于数量关系如何突破呢,其实并没有想象的那么困难,下面小编给大家介绍只需要通过利用题干快速解题的方法。
一、方法介绍
虽然数量关系难,但是对于大部分题目而言,题干中都会存在等量关系,通过建立等量关系来解决。
二、例题展示
例1老师在课堂上出了18道速算题,规定学生答对一道题得6分,答错一道题倒扣1分。一位学生全部答完,得了94分,问他答对了多少道题?
A.12 B.14 C.16 D.17
【解析】C。根据题目可以发现题干告诉了我总题量和总的得分数,那么可以根据此建立等量关系。设答对和答错的题量分别为x和y,则满足
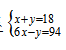
,解之得x=16。
例2骑自行车从甲地到乙地,以10千米/时的速度行进,下午1时到;以15千米/时的速度行进,上午11时到。如果希望中午12时到,那么应以怎样的速度行进?
A.11千米/时 B.12千米/时 C.12.5千米/时 D.13.5千米/时
【解析】B。这道题告诉了我们行驶同一段路程以不同的速度产生到达时间的差异,那么我们可以通过路程相等建立等量关系。假设上午x时出发,以v的速度前进。等量关系为10⨯(13-x)=15⨯(11-x)=v⨯(12-x),x=7,v=12千米/时。
例3张先生向商店订购某种商品80件,每件定价100元,张先生向商店经理说,“如果你肯减价,每减1元,我就多订购4件”商店经理算了一下,他如果减价5%,那么由于张先生多订购,仍可获得与原来一样的利润,这种商品的成本是多少元?
A、65 B、70 C、75 D、80
【解析】C。这道题讲述了如果按照两种价格购买不同数量的商品产生同样利润的问题,那么我们就可以根据利润相同建立等量关系,设这种商品的成本是x元,那么(100-x)80=(95-x)100,解之得x=75。
根据上边的几个题目,大家可以看到如果我们在题目中能够找到等量关系,可以快速的解题,同时能够求解的题目涉及计算问题、行程问题、利润问题等。大家掌握了这种思维方式不仅可以帮助大家解决一类问题,更可以解决更多的数学问题。
行测类比推理成语题如何解答
作为行测必考题型的类比推理,由于题干较短短,考试时间紧,所以并不是很受考生的重视。但是,如果仔细分析就会发现,虽然题干较简短,但总有些题目是“卧虎藏龙”的。尤其是近些年来类比的题目难度加大,考试形式日益多元化,比如说成语。接下来就为大家总结一下类比推理中考察成语的形式。
一、成语的词义考查
词义的考察可能对于成语来说是最常见和最简单的一种形式。总的概括下来,具体考察的有近义关系、反义关系、褒贬义和成语的含义。那这就要要求我们平时注意成语的的积累,需要了解成语的基本含义。
(1) 近义关系
心猿意马:心烦意乱
A. 颐指气使:怒发冲冠
B. 目无全牛:管中窥豹
C. 举足轻重:举重若轻
D. 程门立雪:尊师重道
【答案】D。解析:首先判断题干词语间关系。心猿意马比喻人的心思散乱,如猿马般难以控制。形容心里东想西想,安静不下来。心烦意乱形容心情烦躁,思绪纷乱,两个成语是近义词。其次:判断选项词语关系。程门立雪指尊敬师长,比喻求学心切和对有学问长者的尊敬。尊师重道指尊敬师长,重视自己的教育事业,与题干关系一致。
(2) 反义关系
出其不意:正中下怀
A. 初生牛犊:胆小如鼠
B. 处心积虑:想方设法
C. 闲言碎语:弦外之音
D. 声色俱厉:和颜悦色
【答案】D。解析:出其不意指出乎对方意料之外,突然行动;正中下怀指正好符合自己的心愿两者为反义关系。 声色俱厉是形容说话时声音和脸色都很严厉,和颜悦色形容和蔼喜悦的脸色,两者为反义关系,与题干逻辑关系一致,当选。
(3)褒贬义
神采奕奕:豁达大度
A. 兢兢业业:眉飞色舞
B. 炯炯有神:赤胆忠心
C. 漫不经心:恬不知耻
D. 心猿意马:忐忑不安
【答案】B。解析:神采奕奕和豁达大度是褒义词,而炯炯有神和赤胆忠心都是褒义词。
(4)成语的含义
美丽:成鱼落雁
A. 独特:举世无双
B. 灵活:身手敏捷
C. 厌恶:嗤之以鼻
D. 粗心:三心二意
【答案】D。解析:沉鱼落雁用来形容美丽,而举世无双用来形容独特。
二、成语的语法关系考查
成语的语法关系主要集中在主谓关系、动宾关系和并列关系三种语法上。考查类型可以是将一个成语拆分成两个部分考查,也可以是给出两个具有相同语法关系的成语,方式相对灵活。
(1)主谓关系
红光:满面
A. 东山:再起
B. 魂牵:梦萦
C. 五光:十色
D. 雨打:芭蕉
【答案】A。解析:红光满面构成主谓关系,东山再起构成主谓关系。D项的雨打芭蕉,芭蕉做宾语,打这个动词在前,故为动宾关系。
(2)动宾关系(并列关系)
丰功:伟绩
A. 生吞:活剥
B. 稳扎:稳打
C. 张冠:李戴
D. 登峰:造极
【答案】D。解析:降龙伏虎是并列关系,并列降龙和伏虎内部之间还构成动宾关系,而登峰和造极内部之间也构成动宾关系。A项的生吞和活剥,B项的稳扎和稳打内部构成的是修饰关系。
三、成语的逻辑关系考查
逻辑关系在成语中的考查主要集中在因果关系和目的关系这两方面。
(1)因果关系
人去:楼空
A. 鸟尽:弓藏
B. 鸢飞:鱼跃
C. 兽聚:鸟散
D. 虎踞:龙盘
【答案】C。解析:人去是楼空的原因,两者为因果关系。鸟尽是弓藏的原因,两者为因果关系。
(2)目的关系
围湖造田:饮鸩止渴
A. 卧薪尝胆:学以致用
B. 忍辱偷生:削足适履
C. 兢兢业业:刻苦奋进
D. 山穷水尽:柳暗花明
【答案】B。解析:围湖的目的是为了造田,饮鸩的目的是为了止渴。题干成语内部之间构成目的关系。选择内部构成目的关系的成语。
四、成语的典故来源考查
许多成语典故讲的都是一些名人名事,故把成语与其相关人物结合出题也是类比推理的考法之一,这种考法考察的就是考生的平时的累积。
奇货可居:吕不韦
A. 一鸣惊人:楚庄王
B.退避三舍:齐桓公
C.围魏救赵:孙武
D.草船借箭:周瑜
【答案】选A。 看这个题目,题干词项之间应属于成语与人物对应的关系。“退避三舍”主人公是公子重耳,“围魏救赵”主人公是孙膑或者庞涓,“草船借箭”主人公是诸葛亮。只有A项对应正确。
行测技巧:巧思削弱型选项能否削弱
在公务员行测的考试当中,判断推理部分分为必然性推理和可能性推理。可能性推理在省考中占比较大,对于可能性推理中的削弱型题目,这一种题型在题目中往往会设置几项迷惑选项,哪个选项是整整真正的削弱选项,或者在迷惑项的干扰下稳准狠地勾选正确选项,;下面,小编就和大家一起来看一道题目,希望对大家有所帮助。
【例】:研究人员采用多项倒退任务对人类的一项大脑功能――“工作记忆”进行训练,所有被试者平均分为四组,分别是无训练组、接受8天、12天、17天训练组,所有被试者(包括无训练组)在训练前后均接受智力测验。研究发现,与无训练组相比,训练组的智力水平得到显著提高,并且接受训练的时间越长,智力水平提高越多。由此得出结论:“工作记忆”训练可以提高智力。以下哪项如果为真,最能削弱上述结论?
A.四组测试者接受训练前的智力水平不一样
B.随着接受训练时间的增长,智力提高的速度在减慢
C.可以通过其他任务对个体“工作记忆”进行训练
D.研究证实多项倒退任务能引起其他大脑功能的改进
【解析】:第一步,总括题干:整个题干是通过一个对比实验研究工作记忆和智力的关系。
第二步,分析题干的论证主线:对工作记忆进行训练,被试者分为训练组(8天,12天,17天)和无训练组;训练组智力提升。最终得出结论,“工作记忆”训练可以提高智力。
第三步,分析漏洞:实验和智力提升两件事同时发生,是否代表两者必然具有因果关系,智力的提升是否会和其他原因有关。
第四步观察选项:A选项是在告诉我们四组测试者的初始智力水平不一样,想由初始智力的不同说明实验不科学,以此进行削弱。但是它是否可以削弱?题干研究的是提升智力,也就是在原始的基础上提升,是一种量的变化,提升了就可以,即与初始值无关。B选项说随着时间的增长,提升的速度变慢,说明智力仍在提升,只是慢了而已,不能削弱。C选项想说明除了多项倒退任务之外,还有其他任务可以进行训练,但是题干没有研究到底有哪些方法可以使智力提升,因此无关。D选项是说明多项倒退任务除了对一项功能有作用,还会引起其他功能的进步,说明最后智力的提升可能是因为改进了身体的其他功能而引发的,也就削弱了工作记忆这项任务的可能性。综上所述,这道题选择D。
通过以上例题的解析,我们知道对于一个题目,有些选项好像是想去削弱,但是我们要理清他是否具有削弱的作用,以此去看是否能够对题干起到作用。有很多的选项是确实有削弱倾向,但是没有起到效果,我们在做题时,要不被迷惑,从题干出发,分析漏洞,逐一排除。
行测资料分析考点:A乘B
行测资料分析,会涉及到很多复杂列式,多数是一些复杂的运算,其中,A×B类型的两数乘法运算是常见的运算题型。很多考生在明知这些很重要的情况下,总是想快速求解却难以实现,对其又爱又恨,又无可奈何。此次带领大家对这种形式进行详细梳理,明确求解思路。
一、数字选取
对于两个数字的乘法运算,比如:38.31×46.44,如果进行精算或者取前三位有效数字来进行计算,计算难度太高,如果取第一位来进行计算,精度不能保证,所以,一般取前两位有效数字进行计算。但是要适当观察第三位有效数字如何取舍,按照常规理解,很多考生会对第三位有效数字都进行四舍五入,比如取43×36来进行,但是这样会导致两个数都变小了,结果变小过多,不可取。所以我们要取两位有效数字来进行运算,重点关注第三位有效数字的取舍原则。
二、取舍原则
第三位有效数字的取舍原则如下:
(1)全舍。若第三位有效数字全为0、1、2,则全舍。
【例1】15117.6×1.413=( )
A.21361 B.19780 C.20990 D.22470
【答案】C。解析:第三位有效数字全为1,则两个1全部舍掉。原式≈15000×1.4=21000,选C。
(2)全进。若第三位有效数字全为8或9,则全进。
【例2】2781.7×1.697=( )
A.3912 B.4231 C.4566 D.4721
【答案】C。解析:第三位有效数字全为8或9,则两个8全进。原式≈2800×1.7=4760,选D。
(3)一进一舍。若第三位有效数字不符合全进全舍,则为一进一舍。一进一舍的规则为前三位有效数字小的数四舍五入,另一个数反向取舍。
【例3】43.47×36.31≈( )
A.1578 B.1431 C.1352 D.1218
【答案】A。解析:第三位有效数字分别为4和3,不符合全进全舍,则为一进一舍。前三位有效数字小的数为36.31,将36.31的第三位有效数字四舍五入,则3小于5,舍掉。因为3舍掉了,所以另一个数43.74的第三位有效数字反向取舍,即向前进1,取44来运算,43.47×36.31≈44×36=1584,选A.
推荐阅读:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |