2．4数形结合思想（用好几何性质）
代表性题型：函数与几何综合题。
例4．在平面直角坐标系xOy中，已知抛物线y=a（x+1）
+c（a＞0）与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，其顶点为M,若直线MC的函数表达式为
,与x轴的交点为N，且COS∠BCO＝
。
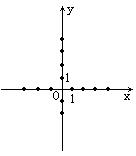
⑴求次抛物线的函数表达式。
(2)在此抛物线上是否存在异于点C的点P，使以N、P、C为顶点的三角形是以NC为一条直角边的直角三角形？若存在，求出点P的坐标：若不存在，请说明理由；
(3)过点A作x轴的垂线，交直线MC于点Q.若将抛物线沿其对称轴上下平移，使抛物线与线段NQ总有公共点，则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
解析：⑴由直线y=kx－3与y轴交点坐标为C（0，－3）
抛物线y=a（x+1）+c（a＞0）开口向上，过C（0，－3）
∴A、B在y轴两侧，B在y轴右侧。如图。
Rt△AOC中，OC=3，cos∠BCO=
∴BC=
，OB=1
∴B（1，0） 又B（1，0），C（0，－3）在y=a（x+1）+c上
∴抛物线解析式y=x+2x－3
⑵由⑴抛物线顶点M（－1，－4），直线y=kx－3过M，∴直线解析式y=x－3
∴N（3，0） ∴△NOC为等腰直角三角形
假设抛物线上存在点P使△NPC为以NC为一条直角边的直角三角形。
①PC为另一条直角边。PC⊥CN，而A与N关于y轴对称在抛物线上。
∴存在P1（－3，0）使△NPC为以NC为一条直角边的直角三角形
②PN为另一条直角边。PN⊥CN，则∠PNO=45°设PN交y轴于点D，则D（0，3）
PN所在直线y=－x+3
由
解得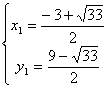
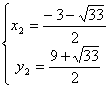
∴存在P2（
，
），P3（
，
）使△NPC为以NC为一条直角边的直角三角形。
满足条件的点有P1（－3，0），P2（，），P3（，）
⑶①若抛物线沿对称轴向上平移。设向上平移b个单位（b＞0）。
此时抛物线的解析式为：y=x+2x－3+b
抛物线与线段NQ总有交点，即由抛物线解析式、直线MC所在直线解析式组成的方程组有解。由
消除y得x+x+b=0，
Δ=1－4b≥0， ∴0＜b≤
∴向上最多可平移个单位
②若向下平移b个单位（b＞0），设y=x+2x－3－b
由y=－x+3，可求得Q（－3，－6），N（3，0）
对于抛物线y=x+2x－3－b
当x＝－3，y=－b，抛物线与直线y=－x+3有交点，则需－b≥-6，b≤6
当x=3时，y=12－b，抛物线与直线y=－x+3有交点，则12-b≥0，b≤12。
∴向下最多可平移12个单位。
思想方法解读：本题还是一道二次函数与平面几何综合的压轴题。
第⑴问中，由直线解析式求出C点坐标，由C点坐标结合a＞0，判定抛物线与x轴交点的大致位置。并结合cos∠BCO=，求出B点坐标，在根据待定系数法求出抛物线的解析式。
第⑵问，以NC为直角边的直角三角形，应分C、N分别为直角顶点分类讨论。结合相应点的坐标及垂直条件，利用45°角的几何性质，分析得到A点满足条件，并求出PN⊥NC时，PN所在直线的解析式，是解题的关键。
第⑶问是本题的难点。分抛物线向上、向下平移两种讨论。向上平移时，需抛物线与直线NQ有交点，由判别式可确定平移b的范围；向下平移时，线段NQ是否与抛物线相交，关键是两个端点N、Q是否在抛物线外侧。只要取两个端点刚好在抛物线上的特殊情况，进行分别判断，求出满足条件的b的范围即可，体现出用极端值解题的思想。
由以上的试题可看出，在中考压轴题中所体现出的数学思想方法并不是单一的，一般每道中考压轴题均综合体现了两到三种不同的数学思想方法。我们在求解压轴题时，一定要结合题型特征，注意一些常见的数学思想方法的灵活运用。
作者简介：宋毓彬，男，43岁，中学数学高级教师。在《中学数学教学参考》、《数理天地》、《中学生数学》、《数理化学习》、《数理化解题研究》、《中学课程辅导》、《数学周报》、《数学辅导报》、《数理报》、《少年智力开发报》、《学习报》、《小博士报》等报刊发表教学辅导类文章60多篇。主要致力于初中数学中考及解题方法、技巧等教学方面的研究。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |