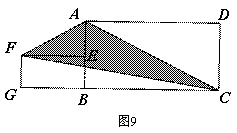
3．（2008黑龙江鸡西）如图9，矩形
中，
cm，
cm，点
为
边上的任意一点，四边形
也是矩形，且
，则
．
解析：这是一道关于长方形的，但也有特殊的地方（两个长方形的长宽比都是2∶1）．下面给出五种做法供大家探讨．
3.1解法一：如图9，设FG=a cm，则FE=2a cm，
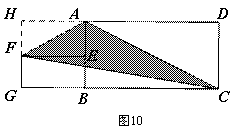
3.2解法二：如图10，设FG=a cm，则FE=2a cm，
3.3解法三：如图11，∵FB∥AC(易证)
∴
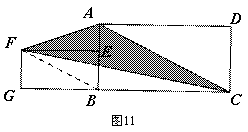
(同底等高)
∴
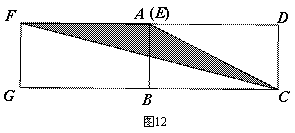
3.4解法四：如图12，用动态的眼光看问题当点E与点A重合时，可得：
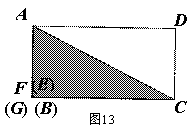
3.5解法五：如图13，用动态的眼光看问题当点E与点B重合时右边的长方形变为一点，可得：
点评 上面3．4不一定简单，但也是一种方法．作为一个填空题3.1、3.2、3.4是不可取的有点复杂，3.3、3.5相应的简单些．
看了这么多解题的例子，学会了吗？下面我给两道题大家练一练．看你能用几种方法解下面的问题．
快乐体验：
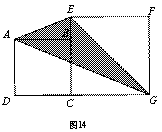
1．如图14：把下面两个正方形放在一起，右边的大正方形边长是10cm，求阴影部分△BDF面积．
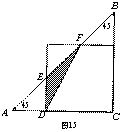
2．如图15，△ABC是一个等腰直角三角形，它与一个正方形叠放在一起，已知AE、EF、FB三条线段一样长，△EFD（阴影部分）面积是4平方厘米，求△ABC面积是多少？
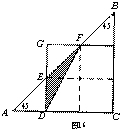
（提示：如图16，根据“同底等高”原理，△ADE的面积=△DEF的面积=△EGF的面积，它们的面积都等于4平方厘米．再将正方形切割成四个小正方形，不难看出，每个小正方形的面积等于两个△EGF的面积，而大三角形ABC则是由9个小三角形组成．于是就能算出大三角形的面积了．）
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |