与方形相关的“面积”的多种求法
与方形相关的求平面图形的“阴影”部分的面积是近年中考中比较常见的问题．求“阴影”部分的面积最能体现数学思维方法的灵活性与技巧性．
最近，我老是看到有关这类题目的文章，其解法也是比较单一的且比较复杂的．有好的解题方法对于考试来说是至关重要的，好的方法意味着即省时间又能准确地做对．
华罗庚先生说：神奇化易是良训，易化神奇不足提！下面我们一起来赏析一下这类题目的几种不同解法，比较一下各种方法的优劣，学习一下“神奇化易”的本领．
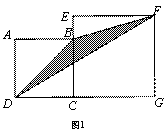
1．（小学数学题）如图1：把下面两个正方形放在一起，左边的小正方形边长是10cm，求阴影部分△BDF面积．
解析：这是一道小学里的题目，作为初中生的你该怎么做这道题呢？可能你还不会，也可能你的方法不只一种．下面我们一起来研究．
1.1解法一：如图2，你也许想到了设未知数，采用整个图形的面积减去空白部分的面积，剩下的就是所求阴影部分的面积的方法．我们来一起做一下．
设EF=a cm ，得：
+
－
－
－
50
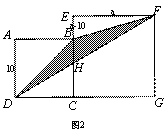
1.2解法二：如图3，可能你会联想到平行线具有“传递面积”的功能(等底等高的三角形面积相等)，于是我 们 连 接CF ，得：
∵BD∥FC．所以△BDF与△BDC，等底同高面积相等．
∴
1.3解法三：如图4，可你能想到了这样的做法吗？从动态的角度看问题．由上面的两种解法（或者说题目中没告诉正方形EFGC的边长）我们能看出来△BDF的面积与右边的正方形EFGC的边长没有关系．也就是说正方形EFGC的边长是可以变化的，但是正方形EFGC的边长是有取值范围的即EF≧AB．当EF=AB时，是比较特殊的情况如图4，不难看出此时
50
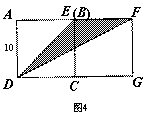
点评 上面是一道小学的题目，对于一般的中学生来说解决它也许不成问题．上面的不同方法代表了不同的数学思想，1.1代数思想、1.2几何思想、1.3动态思想(特殊值法)运用不同的思想其繁简程度的不同是显而易见的．
接下来是一道2010年广西南宁的中考题，下面我们运用上面的三种思想（1.1代数思想、1.2几何思想、1.3动态思想(特殊值法)）做这道题，比较一下各种方法用于这道题的优劣．
2．（2010广西南宁）如图5，正方形
、正方形
和正方形
的位置如图5所示，点
在线段
上，正方形的边长为4，则
的面积为：（ ）
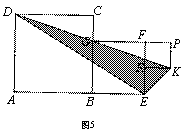
（Ａ）10 （Ｂ）12 （Ｃ）14 （Ｄ）16
解析：这道题目可以看做上面一题的变式扩展，我们同样用上述思想来完成这道题目看有没有新的发现．
2.1解法一：如图6，先把它填补成规则的图形，再用整个图形的面积减去空白部分的面积，剩下的就是所求阴影部分的面积．
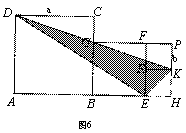
设左边的大正方形ABCD的边长为a，右边的小正方形的边长为b，则KH=（4－ｂ），
－
－
－
－
． 故应选D ．
2.2解法二：如图6，或许有些学生认为上面求
的表达式比较麻烦，他们注意到四边形AHKD是一个梯形，这样可表示为
，表达式变得简单多了．于是
．
由于已知条件并没有直接告诉4 a －4 b的值，有的同学做到这里“卡壳”了．怎么办呢?下面的事情就是求出4 a －4 b的值，为此需要找出a，b的关系．注意到△DCG ～△GPK，则有
，即
．整理得：4a－4b=16．从而可得． 故应选D ．
所以从表面上看，将S△DEK 的表达式变得简单了，似乎求解过程也应该简单．然而在求解过程中，还需用到相似三角形的知识，不仅麻烦有时甚至在这里“卡壳”．
2.3解法三：如图7，利用“传递面积”的功能(等底等高的三角形面积相等)，于是我们连接DB、GE、FK，得：△GED的面积等于△GEB的面积、△GEF的面积等于△GEK的面积．
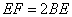
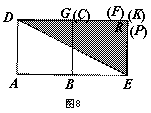
2.4解法四：如图8，利用动态思想(特殊值法)．因为题目中没有告诉左边的正方形ABCD和右边正方形FPKR的边长大小，说明所求结果与其大小是没有关系的，其边长大小是可以变化的但是有范围（CD≧GF＞PF）．用特殊值法，当CD=GF时得到图8，（注意：正方形ABCD的边长变化过程中因为点在线段上，所以GF是不可能等于PF的，四边形FPKR也不总是正方形的．）此时左边的正方形和中间的正方形全等右边的正方形变为一点．有图可知：
点评 这是一道选择题在考试的时候，用前面的两种方法显然是不可取的（计算量大，费时且容易出错．）后两种方法虽然简单易行，可一般的考生不容易想到．
再看一道题，它是2008年黑龙江鸡西的一道中考填空题．前面两道都是关于正方形的而这一道是关于长方形的，也可以看成第一道题的变式．下面我们来做一做．
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |