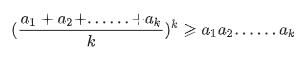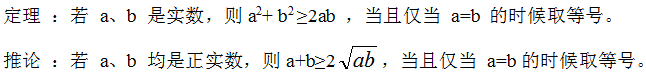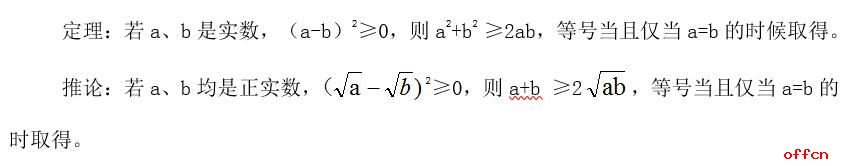从初中开始就已经学习了简单的不等式,到高中深入学习,又有了均值不等式,下面是由出国留学网编辑为大家整理的“高中四个均值不等式推导过程详解”,仅供参考,欢迎大家阅读本文。
高中四个均值不等式推导过程详解
四个均值不等式
1、调和平均数:Hn=n/(1/a1+1/a2+...+1/an)
2、几何平均数:Gn=(a1a2...an)^(1/n)
3、算术平均数:An=(a1+a2+...+an)/n
4、平方平均数:Qn=√ (a1^2+a2^2+...+an^2)/n
这四种平均数满足Hn≤Gn≤An≤Qn 的式子即为均值不等式。
均值不等式用数学归纳法的证明
第一步:等价变换,分子增加又减去同一项,巧妙处是这一项指数的选取,正好是要证明的右端。
第二步:(1)把前面(a1+a2+...+ak)用上面假设n=k成立时较小的右端乘k代替,(a1+a2+...+ak)/k≥(a1a2...ak)^(1/k),两边乘k:
a1+a2+...+ak≥k(a1a2...ak)^(1/k),
因此≥成立。
(2)难点是a(k+1)+(k-1)(a1a2...a(k+1))^(1/(k+1))≥k[a(k+1)(a1a2...a(k+1))^[(k-1)/(k+1)]]^(1/k)
其实也很好证明(k-1)(a1a2...a(k+1))^(1/(k+1),看成是k-1个数,加上a(k+1),也是k个数。
根据上面假设,n=k时,(a1+a2+...+ak)/k≥(a1a2...ak)^(1/k)是成立的,
注意!!!a1,a2,...,ak只是正数的代表,不限于什么正数,换成k个数:a(k+1),和k-1个(a1a2...a(k+1))^(1/(k+1),这个不等式也是成立的!代换一下,就成了:
a(k+1)+(k-1)(a1a2...a(k+1))^(1/(k+1))≥k[a(k+1)(a1a2...a(k+1))^[(k-1)/(k+1)]]^(1/k)
第三步:
前面两项提取k之后成为:
(a1a2...ak)^(1/k)+[a(k+1)(a1a2...a(k+1))^[(k-1)/(k+1)]]^(1/k)
使用前面一开始证明的n=2时的结果,a1+a2≥2√(a1a2)(当成公式,不是当成数)
(a1a2...ak)^(1/k)+[a(k+1)(a1a2...a(k+1))^[(k-1)/(k+1)]]^(1/k)
≥2{(a1a2...ak)^(1/k)[a(k+1)(a1a2...a(k+1))^[(k-1)/(k+1)]]^(1/k)}^(1/2)
=2{(a1a2...ak)^(1/k)[a(k+1)^(1/k)(a1a2...a(k+1))^[(k-1)/k(k+1)]]}^(1/2)
=2{(a1a2...ak)^(1/k)[a(k+1)^(1/k)(a1a2...a(k+1))^[1/(k+1)-1/k(k+1)]]}^(1/2)