在考场上人与人拉开差距的除了平常的知识点的积累,还有面对考试题型能够有一个更好的解答思路,下面由出国留学网小编为你精心准备了“行测数量关系技巧:求解二元一次不定方程之三看法”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:求解二元一次不定方程之三看法
在行测备考过程中,行测理科数量关系里对应的计算问题、行程问题、利润问题、工程问题、年龄问题等,几乎一次考试中的大部分数量关系的题目都可以用方程法去完成。若是找到等量关系,设好未知数,方程列出来,就算不会解,我们也可以将选项带入排除,从而找到那个唯一的正确选项。普通方程对于我们的考生而言,是很容易解的,但解不定方程,有些学员就有点迷糊了。在这里给大家介绍二元一次不定方程的解法——三看法,熟练操作几次,相信你再也不怕不定方程了。
一、认识不定方程
1.方程
含有未知数的等式,叫方程。例如:
2.不定方程
未知数的个数超过独立方程的个数,这样的方程叫不定方程。(独立方程,简言之就是这个方程能否由其他方程线性组合得到,如果能,则不是独立方程,如果不能,则是独立方程。)例如:
这个方程也叫二元一次不定方程,因为它未知数的个数有两个,且未知数的次数都是1,这样的方程是我们现在研究的重点。
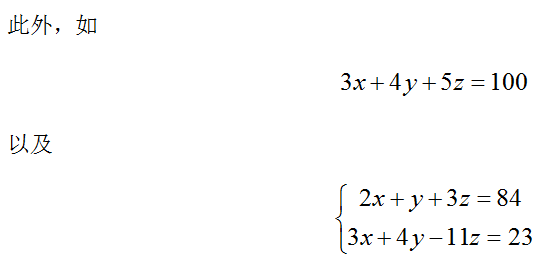
这样的方程都叫做不定方程。
3.不定方程的解
能够让方程左右两边相等的未知数的值叫做方程的解。在这里,主要介绍数量关系中最常见的二元一次不定方程的解的求法。例如:

可见,在实数范围里,这样的不定方程的解有无数组。但是在数量关系的应用题当中,我们借助不定方程去解一些应用题的时候,往往是在正整数范围里去解方程。在正整数里去解这样的二元一次方程,它的解往往只有一个或者有限个解。
二、求不定方程的解
1.求解方法
案例一:在正整数范围里去求解这个方程:
一看,x和y前面的系数有没有偶数——限定未知数的奇偶性。经观察,x前面的系数是2,2是偶数,所以无论x取到什么正整数,2x这一项一定是偶数。再看常数项21,是奇数。由于偶数加上奇数才能得到奇数,所以7y这一项必为奇。由此判定y必为奇数,因为y若为偶,7y也为偶了,不符合要求。
y限定为奇数,y只能等于1、3、5···,当y=1时,x=7;当y=3时,x=0,不是正整数,排除;当y=5时,x也不是正整数,往后更加不可能。因此,在正整数范围里,它只有唯一的一组解,就是x=7,y=1.
下面,再举一个例子,来一起感受三看法解题的快捷准确性。
案例二:在正整数范围里去求解这个方程:
一看,x和y前面的系数有没有偶数——限定未知数的奇偶性。4是偶数,4y这一项必为偶,32是偶数,偶数+偶数=偶数,因此5x这一项也必为偶数,x必为偶数。
二看,x和y前面的系数有没有5的倍数——尾数(个位数)。x前面的系数是5,是5的1倍,所以5x这一项的尾数一定是0或者5,根据刚才的结论,5x这项为偶,所以5x的尾数一定是0。32的尾数是2,根据0+2=2,得4y的尾数一定是2.从而限定了y的范围,y=3,8,13,18,23,28······代入方程,y=3才能让x是正整数,此时,x=4。因此这个方程的解为:x=4,y=3。
此外,这个方程还可以限定x的范围,我们可以:
三看,未知数的系数和常数项这三个数有没有公共因子(公约数)——利用整除去求解。5,4和32,这三个数,我们发现4和32这两个数有公共因子4,这两项都可以被4整除,那么5x这一项也必能被4整除。又由于5不能被4整除,所以x一定能被4整除。X的范围也限定了。x=4,8,······,x只能等于4,才能让y是正整数,此时y=3.因此这个方程的解为:x=4,y=3。
2.方法总结
在正整数范围里求二元一次不定方程的解。一看x和y前面的系数有没有偶数——限定未知数的奇偶性;二看x和y前面的系数有没有5的倍数——尾数(个位数)法限定未知数的范围;三看,未知数的系数和常数项这三个数有没有公共因子(公约数)——利用整除法进一步去限定未知数的范围。
三、方法应用
例1.校学生会组织篮球和足球比赛,需要篮球和足球总数不超过20个,篮球80元一个,足球50元一个,买两种球共花去2420元,问,买篮球多少个?
A.16 B.17 C.18 D.19
[解析]两种球共花去2420元建立等量关系。设篮球买了x个,足球买了y个。根据等量关系列出方程:
,化简这个方程得到:
。接下来解此二元一次不定方程:一看系数有8,是偶数,8x这项必为偶,242是偶数,则5y这项必为偶,y必为偶数。二看,5是5的倍数,结合尾数,5y的尾数一定为0,2+0=2,则8x的尾数定为2,结合选项只有19×8满足尾数是2。因此答案选D。此外,这个题方程得出之后,直接将选项一个一个代入,满足题目中正整数及和不超过20的要求即可。
例2.某超市将99个苹果进行包装,恰好用十多个盒子装完。大包装盒每个装12个苹果,小包装盒每个装5个苹果,每个盒子刚好装满。问这两种包装盒相差多少个?
A.3 B.4 C.7 D.13
[解析]题目中存在着大包装盒装的苹果数加上小包装盒装的苹果数的和是99个,这样的等量关系。设大包装盒用了x个,小包装盒用了y个。得到方程:
。x和y都是正整数,且和在10到20之间。解方程:一看x前的系数有12是偶数,12x这项必为偶数,99是奇数。偶数加奇数才能得奇数,因此5y必为奇数,y必为奇数。二看y前有5,结合奇数性,5y的尾数必为5,99的尾数是9,由于4+5=9,得12x的尾数必为4,x的范围限定为2,7,12,17,22,27······依次代入,找到x=2时,y=15,当x=7时,y=3.再结合和在10和20之间,排除第二组解。正确的答案就出来了,x=2,y=15,大小包装盒数量差为13,因此本题选D。此外,本题,也可三看有没有公共因子。12和99都有公约数3,因此,12x和99都能被3整除,5y也必能被3整除,y必能被3整除,y的范围限定为3,6,9,12,15,18······,依次代入找到满足题目要求的唯一的那个解,求得当y=15的时候,x=2满足题意。因此,本题答案选D。
通过以上题目练习,大家熟练掌握了三看法了吗?对于其中原理感兴趣的学员可以查阅相应的同余定理相关资料。在我们备考的过程中,碰到的二元一次不定方程的情况较多,还有少许其他不定方程,比如说三元一次不定方程组,解法多样,其中最简单的就是直接令其中一个系数较复杂的那个未知数为0,然后在实数范围里去解普通方程组,从而找到要求的那个固定值。总之,遇到二元一次不定方程不要怕,代入排除法配合三看法包你一定能够解出来。注意具体题目具体分析,有的不定方程一看就限定了范围找到了答案,有的不定方程一看、二看加三看才能限定范围找到那个答案,大家要记得灵活使用此三看法。
推荐阅读:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |