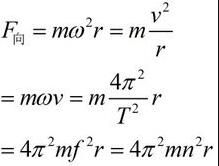数学的公式都是由简单到复杂的,很多时候,我们学着学着就学不下去了,其实最主要的还是公式不够了解,出国留学网的小编现在就带你们去看看这二倍角公式如何推导,感兴趣的朋友们不要错过了哦。
二倍角公式如何推导
正弦二倍角公式:sin2α=2cosαsinα
推导:
sin2α=sin(α+α)=sinαcosα+cosαsinα=2sinαcosα
余弦二倍角公式:
余弦二倍角公式有三组表示形式,三组形式等价:
1.cos2α=2cos^2α-1
2.cos2α=1−2sin^2α
3.cos2α=cos^2α−sin^2α
推导:
cos2A=cos(A+A)=cosAcosA-sinAsinA=cos^2A-sin^2A=2cos^2A-1=1-2sin^2A
正切二倍角公式:
tan2α=2tanα/[1-(tanα)^2]
tan(1/2*α)=(sinα)/(1+cosα)=(1-cosα)/sinα
推导:
tan(2a)=tan(a+a)=(tan(a)+tan(a))/(1-tan(a)*tan(a))=2tanα/[1-(tanα)^2]
半角公式推导过程
1、根据倍角公式得:
coa2a=1-2sin2α,可得
cosa=1-2sin2(α/2),可得
1-cosa=2sin2(α/2),可得
sin2(α/2)=(1-cosa)/2,可得,sin((a/2)=根号(1-cosa)/2)
cos2(α/2)=1-sin2(α/2)
所以:cos2(α/2)=1-(1-cosa)/2=(1+cosa)/2
所以:cos(a/2)=根号(1+cosa)/2
因为:tana=sina/cosa
所以:tan(a/2)=sin(a/2)/cos(a/2)
所以:tan(a/2)=根号((1-cosa)/(1+cosa))
2、在cos2α=1-sin2α中,以α代2α,α/2代α,得:
cosα=1-sin2α/2所以sin2α/2=(1-cosα)/2
在cos2α=2cos2α-1中,以α代2α,α/2代α,得
cosα=2cos2(α/2)-1所以cos2(α/2)=(1+cosα)/2
然后以上结果相除
tan2α/2==(1-cosα)/(1+cosα)
1-cosα/sinα=1-(1-sin2α/2)/[2sin(α/2)cos(α/2)]
=2sin(α/2)/cos(α/2)
=tanα/2
二倍角公式如何推导?还有就是半角公式推导过程,出国留学网的小编已经给你们整理好了哦,想要读懂上面的知识的话,你们可能需要花一点点时间哦。
推荐阅读: